MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance beuster
| Formatsⓘ | ams gms mod nl osil py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 116329.67050000 (ANTIGONE) 103117.31250000 (BARON) 29606.18502000 (COUENNE) 105174.35440000 (GUROBI) 116329.67060000 (LINDO) 55563.78422000 (SCIP) 5942.49140900 (SHOT) 10445.97213000 (XPRESS) |
| Sourceⓘ | GAMS Client |
| Applicationⓘ | four membrane pipe modules in feed-and-bleed coupling |
| Added to libraryⓘ | 01 May 2001 |
| Problem typeⓘ | MBNLP |
| #Variablesⓘ | 157 |
| #Binary Variablesⓘ | 52 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 66 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | linear |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 6 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 114 |
| #Linear Constraintsⓘ | 67 |
| #Quadratic Constraintsⓘ | 26 |
| #Polynomial Constraintsⓘ | 8 |
| #Signomial Constraintsⓘ | 9 |
| #General Nonlinear Constraintsⓘ | 4 |
| Operands in Gen. Nonlin. Functionsⓘ | div log |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 391 |
| #Nonlinear Nonzeros in Jacobianⓘ | 159 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 291 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 21 |
| #Blocks in Hessian of Lagrangianⓘ | 9 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 1 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 50 |
| Average blocksize in Hessian of Lagrangianⓘ | 7.333333 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 5.5556e-06 |
| Maximal coefficientⓘ | 1.0000e+07 |
| Infeasibility of initial pointⓘ | 7.98e+04 |
| Sparsity Jacobianⓘ | 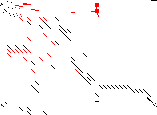 |
| Sparsity Hessian of Lagrangianⓘ |  |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 115 100 12 3 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 158 106 52 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 398 239 159 0
*
* Solve m using MINLP minimizing objvar;
Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51,x52,x53
,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68,x69,x70
,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80,x81,x82,x83,x84,x85,x86,x87
,x88,x89,x90,x91,x92,x93,x94,x95,x96,x97,x98,x99,b100,b101,b102,b103
,b104,b105,b106,b107,b108,b109,b110,b111,b112,b113,b114,b115,b116
,b117,b118,b119,b120,b121,b122,b123,b124,b125,b126,b127,b128,b129
,b130,b131,b132,b133,b134,b135,b136,b137,b138,b139,b140,b141,b142
,b143,b144,b145,b146,b147,b148,b149,b150,b151,objvar,x153,x154,x155
,x156,x157,x158;
Positive Variables x8,x9,x10,x11,x20,x21,x22,x23,x24,x25,x26,x27,x76,x77,x78
,x79,x80,x81,x82,x83,x84,x85,x86,x87,x88,x89,x90,x91,x92,x93,x94,x95
,x96,x97,x98,x99,x153,x154,x155,x156,x157,x158;
Binary Variables b100,b101,b102,b103,b104,b105,b106,b107,b108,b109,b110,b111
,b112,b113,b114,b115,b116,b117,b118,b119,b120,b121,b122,b123,b124
,b125,b126,b127,b128,b129,b130,b131,b132,b133,b134,b135,b136,b137
,b138,b139,b140,b141,b142,b143,b144,b145,b146,b147,b148,b149,b150
,b151;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63,e64,e65,e66,e67,e68,e69,e70
,e71,e72,e73,e74,e75,e76,e77,e78,e79,e80,e81,e82,e83,e84,e85,e86,e87
,e88,e89,e90,e91,e92,e93,e94,e95,e96,e97,e98,e99,e100,e101,e102,e103
,e104,e105,e106,e107,e108,e109,e110,e111,e112,e113,e114,e115;
e1.. objvar - x153 - x154 - x155 - x156 - x157 - x158 =E= 3271.22725820856;
e2.. x8 =E= 1800;
e3.. x12 =E= 5;
e4.. -(x99*(x24 + x25 + x26 + x27) + (x98 - x99)*(x24 + x25 + x26) + (x97 - x98
)*(x24 + x25) + x24*(x96 - x97)) + x2 =E= 0;
e5.. -((x28*x24 + x29*x25 + x30*x26 + x31*x27)*x99 + (x28*x24 + x29*x25 + x30*
x26)*(x98 - x99) + (x28*x24 + x29*x25)*(x97 - x98) + x28*x24*(x96 - x97))/
x2 + x3 =E= 0;
e6.. -(x19*x99 + x18*(x98 - x99) + x17*(x97 - x98) + x16*(x96 - x97)) + x1
=E= 0;
e7.. -(x23*x99 + x22*(x98 - x99) + x21*(x97 - x98) + x20*(x96 - x97)) =E= -100;
e8.. -(x16*x97 - 1000*x97) + x9 =E= 1000;
e9.. -(x20*x97 - 10*x97) + x13 =E= 10;
e10.. -(x99*(x32 + x33 + x34 + x35) + (x98 - x99)*(x32 + x33 + x34) + (x97 -
x98)*(x32 + x33) + x32*(x96 - x97)) + x5 =E= 0;
e11.. -(x99*(x36 + x37 + x38 + x39) + (x98 - x99)*(x36 + x37 + x38) + (x97 -
x98)*(x36 + x37) + x36*(x96 - x97)) + x6 =E= 0;
e12.. -(x99*(x92 + x93 + x94 + x95) + (x98 - x99)*(x92 + x93 + x94) + (x97 -
x98)*(x92 + x93) + x92*(x96 - x97)) + x7 =E= 0;
e13.. -(x99*(x72 + x73 + x74 + x75) + (x98 - x99)*(x72 + x73 + x74) + (x97 -
x98)*(x72 + x73) + x72*(x96 - x97)) + x4 =E= 0;
e14.. -(x17*x98 - 1058*x98) + x10 =E= 1058;
e15.. -(x21*x98 - 10*x98) + x14 =E= 10;
e16.. -(x18*x99 - 1008*x99) + x11 =E= 1008;
e17.. -(x22*x99 - 13*x99) + x15 =E= 13;
e18.. 0.00277777777777778*x40/log((x44 - x28)/(x20 - x28)) - 10000000*x56 =E= 0
;
e19.. 0.00277777777777778*x41/log((x45 - x29)/(x21 - x29)) - 10000000*x57 =E= 0
;
e20.. 0.00277777777777778*x42/log((x46 - x30)/(x22 - x30)) - 10000000*x58 =E= 0
;
e21.. 0.00277777777777778*x43/log((x47 - x31)/(x23 - x31)) - 10000000*x59 =E= 0
;
e22.. 50*x28 - x44 =E= 0;
e23.. 50*x29 - x45 =E= 0;
e24.. 50*x30 - x46 =E= 0;
e25.. 50*x31 - x47 =E= 0;
e26.. x40 - 65.38084341288*x48 + 65.38084341288*x60 =E= 0;
e27.. x41 - 65.38084341288*x49 + 65.38084341288*x61 =E= 0;
e28.. x42 - 65.38084341288*x50 + 65.38084341288*x62 =E= 0;
e29.. x43 - 65.38084341288*x51 + 65.38084341288*x63 =E= 0;
e30.. - x60 + x64 - 1000*x68 =E= 0;
e31.. - x61 + x65 - 1000*x69 =E= 0;
e32.. - x62 + x66 - 1000*x70 =E= 0;
e33.. - x63 + x67 - 1000*x71 =E= 0;
e34.. -1e-5*(12.09*sqr(x44) + 3.66*x44 - 0.08*x44**3 + 0.0002592*x44**4) + x64
=E= 0;
e35.. -1e-5*(12.09*sqr(x45) + 3.66*x45 - 0.08*x45**3 + 0.0002592*x45**4) + x65
=E= 0;
e36.. -1e-5*(12.09*sqr(x46) + 3.66*x46 - 0.08*x46**3 + 0.0002592*x46**4) + x66
=E= 0;
e37.. -1e-5*(12.09*sqr(x47) + 3.66*x47 - 0.08*x47**3 + 0.0002592*x47**4) + x67
=E= 0;
e38.. -1e-5*(12.09*sqr(x28) + 3.66*x28 - 0.08*x28**3 + 0.0002592*x28**4)
+ 1000*x68 =E= 0;
e39.. -1e-5*(12.09*sqr(x29) + 3.66*x29 - 0.08*x29**3 + 0.0002592*x29**4)
+ 1000*x69 =E= 0;
e40.. -1e-5*(12.09*sqr(x30) + 3.66*x30 - 0.08*x30**3 + 0.0002592*x30**4)
+ 1000*x70 =E= 0;
e41.. -1e-5*(12.09*sqr(x31) + 3.66*x31 - 0.08*x31**3 + 0.0002592*x31**4)
+ 1000*x71 =E= 0;
e42.. -0.000113572384718704*(7936.50793650794*x52)**0.75 + 10000000*x56 =E= 0;
e43.. -0.000113572384718704*(7936.50793650794*x53)**0.75 + 10000000*x57 =E= 0;
e44.. -0.000113572384718704*(7936.50793650794*x54)**0.75 + 10000000*x58 =E= 0;
e45.. -0.000113572384718704*(7936.50793650794*x55)**0.75 + 10000000*x59 =E= 0;
e46.. - x8 + x16 + x24 =E= 0;
e47.. - x9 + x17 + x25 =E= 0;
e48.. - x10 + x18 + x26 =E= 0;
e49.. - x11 + x19 + x27 =E= 0;
e50.. x12*x8 - (x20*x16 + x28*x24) =E= 0;
e51.. x13*x9 - (x21*x17 + x29*x25) =E= 0;
e52.. x14*x10 - (x22*x18 + x30*x26) =E= 0;
e53.. x15*x11 - (x23*x19 + x31*x27) =E= 0;
e54.. -2.77777777777778e-5*x48*x8 + x84 =E= 0;
e55.. -2.77777777777778e-5*x49*x9 + x85 =E= 0;
e56.. -2.77777777777778e-5*x50*x10 + x86 =E= 0;
e57.. -2.77777777777778e-5*x51*x11 + x87 =E= 0;
e58.. -x24/x40 + x72 =E= 0;
e59.. -x25/x41 + x73 =E= 0;
e60.. -x26/x42 + x74 =E= 0;
e61.. -x27/x43 + x75 =E= 0;
e62.. x32 - 20*x72 =E= 0;
e63.. x33 - 20*x73 =E= 0;
e64.. x34 - 20*x74 =E= 0;
e65.. x35 - 20*x75 =E= 0;
e66.. - 373.932*x52 + x76 =E= 0;
e67.. - 373.932*x53 + x77 =E= 0;
e68.. - 373.932*x54 + x78 =E= 0;
e69.. - 373.932*x55 + x79 =E= 0;
e70.. -x32*x76 + x80 =E= 0;
e71.. -x33*x77 + x81 =E= 0;
e72.. -x34*x78 + x82 =E= 0;
e73.. -x35*x79 + x83 =E= 0;
e74.. - 5.55555555555556E-6*x80 + x88 =E= 0;
e75.. - 5.55555555555556E-6*x81 + x89 =E= 0;
e76.. - 5.55555555555556E-6*x82 + x90 =E= 0;
e77.. - 5.55555555555556E-6*x83 + x91 =E= 0;
e78.. - 1.58730158730159*x84 - 1.58730158730159*x88 + x92 =E= 0;
e79.. - 1.58730158730159*x85 - 1.58730158730159*x89 + x93 =E= 0;
e80.. - 1.58730158730159*x86 - 1.58730158730159*x90 + x94 =E= 0;
e81.. - 1.58730158730159*x87 - 1.58730158730159*x91 + x95 =E= 0;
e82.. x36 - 0.909090909090909*x88 =G= 0;
e83.. x37 - 0.909090909090909*x89 =G= 0;
e84.. x38 - 0.909090909090909*x90 =G= 0;
e85.. x39 - 0.909090909090909*x91 =G= 0;
e86.. x32 - b100 - 2*b104 - 4*b108 - 8*b112 - 16*b116 - 32*b120 - 64*b124
- 128*b128 =E= 0;
e87.. x33 - b101 - 2*b105 - 4*b109 - 8*b113 - 16*b117 - 32*b121 - 64*b125
- 128*b129 =E= 0;
e88.. x34 - b102 - 2*b106 - 4*b110 - 8*b114 - 16*b118 - 32*b122 - 64*b126
- 128*b130 =E= 0;
e89.. x35 - b103 - 2*b107 - 4*b111 - 8*b115 - 16*b119 - 32*b123 - 64*b127
- 128*b131 =E= 0;
e90.. x36 - b132 - 2*b136 - 4*b140 - 8*b144 =E= 0;
e91.. x37 - b133 - 2*b137 - 4*b141 - 8*b145 =E= 0;
e92.. x38 - b134 - 2*b138 - 4*b142 - 8*b146 =E= 0;
e93.. x39 - b135 - 2*b139 - 4*b143 - 8*b147 =E= 0;
e94.. x96 - b148 =E= 0;
e95.. x97 - b149 =E= 0;
e96.. x98 - b150 =E= 0;
e97.. x99 - b151 =E= 0;
e98.. b148 =E= 1;
e99.. - b148 + b149 =L= 0;
e100.. - b149 + b150 =L= 0;
e101.. - b150 + b151 =L= 0;
e102.. - 1261.75908530902*x96 - 1261.75908530902*x97 - 1261.75908530902*x98
- 1261.75908530902*x99 + x153 =E= 0;
e103.. - 292.07386234005*x6 + x154 =E= 0;
e104.. - 2103.94993266178*x7 + x157 =E= 0;
e105.. - 45.7380420143865*x2 + x155 =E= 0;
e106.. -4.57380420143865*x2*x3 + x156 =E= 0;
e107.. - 764.973851088085*x4 + x158 =E= 0;
e108.. x20 - x28 =G= 0.01;
e109.. x21 - x29 =G= 0.01;
e110.. x22 - x30 =G= 0.01;
e111.. x23 - x31 =G= 0.01;
e112.. - x28 + x44 =G= 0.01;
e113.. - x29 + x45 =G= 0.01;
e114.. - x30 + x46 =G= 0.01;
e115.. - x31 + x47 =G= 0.01;
* set non-default bounds
x1.lo = 10;
x2.lo = 0.001;
x3.lo = 1;
x4.lo = 1;
x5.lo = 2;
x6.lo = 1;
x7.lo = 0.1675;
x12.lo = 5;
x13.lo = 5;
x14.lo = 5;
x15.lo = 5;
x16.lo = 1;
x17.lo = 1;
x18.lo = 1;
x19.lo = 1;
x28.lo = 0.001;
x29.lo = 0.001;
x30.lo = 0.001;
x31.lo = 0.001;
x32.lo = 1;
x33.lo = 1;
x34.lo = 1;
x35.lo = 1;
x36.lo = 1;
x37.lo = 1;
x38.lo = 1;
x39.lo = 1;
x40.lo = 1;
x41.lo = 1;
x42.lo = 1;
x43.lo = 1;
x44.lo = 0.01;
x45.lo = 0.01;
x46.lo = 0.01;
x47.lo = 0.01;
x48.lo = 2; x48.up = 6;
x49.lo = 2; x49.up = 6;
x50.lo = 2; x50.up = 6;
x51.lo = 2; x51.up = 6;
x52.lo = 1.33; x52.up = 6;
x53.lo = 1.33; x53.up = 6;
x54.lo = 1.33; x54.up = 6;
x55.lo = 1.33; x55.up = 6;
x56.lo = 1.13E-8;
x57.lo = 1.13E-8;
x58.lo = 1.13E-8;
x59.lo = 1.13E-8;
x60.lo = 2.9E-7;
x61.lo = 2.9E-7;
x62.lo = 2.9E-7;
x63.lo = 2.9E-7;
x64.lo = 3E-7;
x65.lo = 3E-7;
x66.lo = 3E-7;
x67.lo = 3E-7;
x68.lo = 3E-10;
x69.lo = 3E-10;
x70.lo = 3E-10;
x71.lo = 3E-10;
x72.lo = 0.05;
x73.lo = 0.05;
x74.lo = 0.05;
x75.lo = 0.05;
* set non-default levels
x1.l = 67.344;
x2.l = 1744.656;
x3.l = 3.042;
x4.l = 12.808;
x5.l = 216.161;
x6.l = 1.225;
x7.l = 3.842;
x8.l = 1800;
x9.l = 241.731;
x10.l = 158.011;
x11.l = 88.847;
x12.l = 10;
x13.l = 12.176;
x14.l = 14.048;
x15.l = 16.416;
x20.l = 12.176;
x21.l = 14.048;
x22.l = 16.416;
x23.l = 18;
x28.l = 1.956;
x29.l = 1.317;
x30.l = 1.737;
x31.l = 1.248;
x32.l = 176.503;
x33.l = 10.861;
x34.l = 11.542;
x35.l = 17.256;
x40.l = 176.572;
x41.l = 154.169;
x42.l = 119.85;
x43.l = 60.852;
x44.l = 110.804;
x45.l = 120.863;
x46.l = 130.858;
x47.l = 140.397;
x48.l = 2.5;
x49.l = 2.5;
x50.l = 2.5;
x51.l = 2.5;
x52.l = 4;
x53.l = 4;
x54.l = 4;
x55.l = 4;
x56.l = 2.1769E-8;
x57.l = 2.1769E-8;
x58.l = 2.1769E-8;
x59.l = 2.1769E-8;
x60.l = 1.299;
x61.l = 1.642;
x62.l = 2.167;
x63.l = 3.069;
x64.l = 1.3;
x65.l = 1.643;
x66.l = 2.169;
x67.l = 3.072;
x68.l = 1E-6;
x69.l = 1E-6;
x70.l = 2E-6;
x71.l = 2E-6;
x72.l = 8.825;
x73.l = 0.543;
x74.l = 0.577;
x75.l = 0.863;
x76.l = 1121.796;
x77.l = 1121.796;
x78.l = 1121.796;
x79.l = 1121.796;
x80.l = 198000;
x81.l = 12183.696;
x82.l = 12947.373;
x83.l = 19357.594;
x84.l = 0.2;
x85.l = 0.027;
x86.l = 0.018;
x87.l = 0.01;
x88.l = 1.1;
x89.l = 0.168;
x90.l = 0.122;
x91.l = 0.108;
x92.l = 2.063;
x93.l = 0.15;
x94.l = 0.142;
x95.l = 0.186;
x96.l = 1;
x97.l = 1;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set MINLP $set MINLP MINLP
Solve m using %MINLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc