MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance gasnet
| Formatsⓘ | ams gms mod nl osil py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 3327325.87700000 (ANTIGONE) 6999381.55500000 (BARON) 3148587.09700000 (COUENNE) 2616082.10700000 (GUROBI) 4264881.61900000 (LINDO) 6999381.56200000 (SCIP) 6417617.34900000 (SHOT) 5732342.89800000 (XPRESS) |
| Referencesⓘ | Edgar, T F, Himmelblau, D M, and Lasdon, L S, Example 13.4. In Edgar, T F, Himmelblau, D M, and Lasdon, L S, Optimization of Chemical Processes, McGraw Hill, Boston, 2001, 469-478. |
| Sourceⓘ | GAMS Model Library model gasnet |
| Applicationⓘ | Gas Transmission Network Design |
| Added to libraryⓘ | 01 May 2001 |
| Problem typeⓘ | MBNLP |
| #Variablesⓘ | 90 |
| #Binary Variablesⓘ | 10 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 77 |
| #Nonlinear Binary Variablesⓘ | 10 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | linear |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 3 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 69 |
| #Linear Constraintsⓘ | 25 |
| #Quadratic Constraintsⓘ | 22 |
| #Polynomial Constraintsⓘ | 0 |
| #Signomial Constraintsⓘ | 22 |
| #General Nonlinear Constraintsⓘ | 0 |
| Operands in Gen. Nonlin. Functionsⓘ | |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 263 |
| #Nonlinear Nonzeros in Jacobianⓘ | 130 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 248 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 54 |
| #Blocks in Hessian of Lagrangianⓘ | 2 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 2 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 75 |
| Average blocksize in Hessian of Lagrangianⓘ | 38.5 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 7.5864e-07 |
| Maximal coefficientⓘ | 1.0000e+04 |
| Infeasibility of initial pointⓘ | 1.496e+06 |
| Sparsity Jacobianⓘ |  |
| Sparsity Hessian of Lagrangianⓘ | 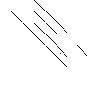 |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 70 49 11 10 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 91 81 10 0 0 0 0 0
* FX 4
*
* Nonzero counts
* Total const NL DLL
* 267 137 130 0
*
* Solve m using MINLP minimizing objvar;
Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51,x52,x53
,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68,x69,x70
,x71,x72,x73,x74,x75,x76,x77,b78,b79,b80,b81,b82,b83,b84,b85,b86,b87
,x88,x89,x90,objvar;
Positive Variables x68,x69,x70,x71,x72,x73,x74,x75,x76,x77;
Binary Variables b78,b79,b80,b81,b82,b83,b84,b85,b86,b87;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63,e64,e65,e66,e67,e68,e69,e70;
e1.. x12 - x24 =G= 0;
e2.. x13 - x25 =G= 0;
e3.. x14 - x26 =G= 0;
e4.. x15 - x27 =G= 0;
e5.. x16 - x28 =G= 0;
e6.. x17 - x29 =G= 0;
e7.. x18 - x30 =G= 0;
e8.. x19 - x31 =G= 0;
e9.. x20 - x32 =G= 0;
e10.. x21 - x33 =G= 0;
e11.. x22 - x34 =G= 0;
e12.. x1 + x2 + x3 + x4 + x5 + x6 + x7 =E= 175;
e13.. x1 + x2 + x3 + x8 + x9 + x10 + x11 =E= 200;
e14.. -7.58641e-7*x35**5.33333333333333*(sqr(x12) - sqr(x24))/sqr(x47) + x1
=E= 0;
e15.. -7.58641e-7*x36**5.33333333333333*(sqr(x13) - sqr(x25))/sqr(x48) + x2
=E= 0;
e16.. -7.58641e-7*x37**5.33333333333333*(sqr(x14) - sqr(x26))/sqr(x49) + x3
=E= 0;
e17.. -7.58641e-7*x38**5.33333333333333*(sqr(x15) - sqr(x27))/sqr(x50) + x4
=E= 0;
e18.. -7.58641e-7*x39**5.33333333333333*(sqr(x16) - sqr(x28))/sqr(x51) + x5
=E= 0;
e19.. -7.58641e-7*x40**5.33333333333333*(sqr(x17) - sqr(x29))/sqr(x52) + x6
=E= 0;
e20.. -7.58641e-7*x41**5.33333333333333*(sqr(x18) - sqr(x30))/sqr(x53) + x7
=E= 0;
e21.. -7.58641e-7*x42**5.33333333333333*(sqr(x19) - sqr(x31))/sqr(x54) + x8
=E= 0;
e22.. -7.58641e-7*x43**5.33333333333333*(sqr(x20) - sqr(x32))/sqr(x55) + x9
=E= 0;
e23.. -7.58641e-7*x44**5.33333333333333*(sqr(x21) - sqr(x33))/sqr(x56) + x10
=E= 0;
e24.. -7.58641e-7*x45**5.33333333333333*(sqr(x22) - sqr(x34))/sqr(x57) + x11
=E= 0;
e25.. x46 - 0.005*x46*b78 - x47 =E= 0;
e26.. x47 - 0.005*x47*b79 - x48 =E= 0;
e27.. x48 - 0.005*x48*b80 - x49 =E= 0;
e28.. x49 - 0.005*x49*b81 - x50 - x54 =E= 0;
e29.. x50 - 0.005*x50*b82 - x51 =E= 0;
e30.. x51 - 0.005*x51*b83 - x52 =E= 0;
e31.. x52 - 0.005*x52*b84 - x53 =E= 0;
e32.. x54 - 0.005*x54*b85 - x55 =E= 0;
e33.. x55 - 0.005*x55*b86 - x56 =E= 0;
e34.. x56 - 0.005*x56*b87 - x57 =E= 0;
e35.. -214.9812*(-1 + x58**0.181587301587302)*x47 + x68 =E= 0;
e36.. -214.9812*(-1 + x59**0.181587301587302)*x48 + x69 =E= 0;
e37.. -214.9812*(-1 + x60**0.181587301587302)*x49 + x70 =E= 0;
e38.. -214.9812*(-1 + x61**0.181587301587302)*x50 + x71 =E= 0;
e39.. -214.9812*(-1 + x61**0.181587301587302)*x54 + x71 =E= 0;
e40.. -214.9812*(-1 + x62**0.181587301587302)*x51 + x72 =E= 0;
e41.. -214.9812*(-1 + x63**0.181587301587302)*x52 + x73 =E= 0;
e42.. -214.9812*(-1 + x64**0.181587301587302)*x53 + x74 =E= 0;
e43.. -214.9812*(-1 + x65**0.181587301587302)*x55 + x75 =E= 0;
e44.. -214.9812*(-1 + x66**0.181587301587302)*x56 + x76 =E= 0;
e45.. -214.9812*(-1 + x67**0.181587301587302)*x57 + x77 =E= 0;
e46.. x58*x23 - x12 =E= 0;
e47.. x59*x24 - x13 =E= 0;
e48.. x60*x25 - x14 =E= 0;
e49.. x61*x26 - x15 =E= 0;
e50.. x61*x26 - x19 =E= 0;
e51.. x62*x27 - x16 =E= 0;
e52.. x63*x28 - x17 =E= 0;
e53.. x64*x29 - x18 =E= 0;
e54.. x65*x31 - x20 =E= 0;
e55.. x66*x32 - x21 =E= 0;
e56.. x67*x33 - x22 =E= 0;
e57.. x58 - b78 =L= 1;
e58.. x59 - b79 =L= 1;
e59.. x60 - b80 =L= 1;
e60.. x61 - b81 =L= 1;
e61.. x62 - b82 =L= 1;
e62.. x63 - b83 =L= 1;
e63.. x64 - b84 =L= 1;
e64.. x65 - b85 =L= 1;
e65.. x66 - b86 =L= 1;
e66.. x67 - b87 =L= 1;
e67.. -(870*x1*x35 + 870*x2*x36 + 870*x3*x37 + 870*x4*x38 + 870*x5*x39 + 870*x6
*x40 + 870*x7*x41 + 870*x8*x42 + 870*x9*x43 + 870*x10*x44 + 870*x11*x45)
+ x88 =E= 0;
e68.. - 70*x68 - 70*x69 - 70*x70 - 70*x71 - 70*x72 - 70*x73 - 70*x74 - 70*x75
- 70*x76 - 70*x77 - 10000*b78 - 10000*b79 - 10000*b80 - 10000*b81
- 10000*b82 - 10000*b83 - 10000*b84 - 10000*b85 - 10000*b86 - 10000*b87
+ x89 =E= 0;
e69.. - 8*x68 - 8*x69 - 8*x70 - 8*x71 - 8*x72 - 8*x73 - 8*x74 - 8*x75 - 8*x76
- 8*x77 + x90 =E= 0;
e70.. - x88 - x89 - x90 + objvar =E= 0;
* set non-default bounds
x1.lo = 2; x1.up = 200;
x2.lo = 2; x2.up = 200;
x3.lo = 2; x3.up = 200;
x4.lo = 2; x4.up = 200;
x5.lo = 2; x5.up = 200;
x6.lo = 2; x6.up = 200;
x7.lo = 2; x7.up = 200;
x8.lo = 2; x8.up = 200;
x9.lo = 2; x9.up = 200;
x10.lo = 2; x10.up = 200;
x11.lo = 2; x11.up = 200;
x12.lo = 200; x12.up = 1000;
x13.lo = 200; x13.up = 1000;
x14.lo = 200; x14.up = 1000;
x15.lo = 200; x15.up = 1000;
x16.lo = 200; x16.up = 1000;
x17.lo = 200; x17.up = 1000;
x18.lo = 200; x18.up = 1000;
x19.lo = 200; x19.up = 1000;
x20.lo = 200; x20.up = 1000;
x21.lo = 200; x21.up = 1000;
x22.lo = 200; x22.up = 1000;
x23.fx = 500;
x24.lo = 200; x24.up = 1000;
x25.lo = 200; x25.up = 1000;
x26.lo = 200; x26.up = 1000;
x27.lo = 200; x27.up = 1000;
x28.lo = 200; x28.up = 1000;
x29.lo = 200; x29.up = 1000;
x30.fx = 600;
x31.lo = 200; x31.up = 1000;
x32.lo = 200; x32.up = 1000;
x33.lo = 200; x33.up = 1000;
x34.fx = 300;
x35.lo = 4; x35.up = 36;
x36.lo = 4; x36.up = 36;
x37.lo = 4; x37.up = 36;
x38.lo = 4; x38.up = 18;
x39.lo = 4; x39.up = 18;
x40.lo = 4; x40.up = 18;
x41.lo = 4; x41.up = 18;
x42.lo = 4; x42.up = 18;
x43.lo = 4; x43.up = 18;
x44.lo = 4; x44.up = 18;
x45.lo = 4; x45.up = 18;
x46.fx = 600;
x47.lo = 200; x47.up = 600;
x48.lo = 200; x48.up = 600;
x49.lo = 200; x49.up = 600;
x50.lo = 200; x50.up = 600;
x51.lo = 200; x51.up = 600;
x52.lo = 200; x52.up = 600;
x53.lo = 200; x53.up = 600;
x54.lo = 200; x54.up = 600;
x55.lo = 200; x55.up = 600;
x56.lo = 200; x56.up = 600;
x57.lo = 200; x57.up = 600;
x58.lo = 1; x58.up = 2;
x59.lo = 1; x59.up = 2;
x60.lo = 1; x60.up = 2;
x61.lo = 1; x61.up = 2;
x62.lo = 1; x62.up = 2;
x63.lo = 1; x63.up = 2;
x64.lo = 1; x64.up = 2;
x65.lo = 1; x65.up = 2;
x66.lo = 1; x66.up = 2;
x67.lo = 1; x67.up = 2;
* set non-default levels
x1.l = 20;
x2.l = 20;
x3.l = 20;
x4.l = 20;
x5.l = 20;
x6.l = 20;
x7.l = 20;
x8.l = 20;
x9.l = 20;
x10.l = 20;
x11.l = 20;
x35.l = 18;
x36.l = 18;
x37.l = 18;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set MINLP $set MINLP MINLP
Solve m using %MINLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc