MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance bayes2_20
| Formatsⓘ | ams gms lp mod nl osil pip py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 0.00000000 (ANTIGONE) 0.00032461 (BARON) 0.00000000 (COUENNE) 0.00000000 (GUROBI) 0.00000000 (LINDO) 0.00000000 (SCIP) 0.00000000 (SHOT) |
| Referencesⓘ | Greenberg, Betsy, Lasdon, L S, and Plummer, John, Using Global Optimization to Estimate Population Class Sizes, Journal of Global Optimization, 36:3, 2006, 319-338. |
| Sourceⓘ | Leon Lasdon |
| Added to libraryⓘ | 31 Jul 2001 |
| Problem typeⓘ | QCP |
| #Variablesⓘ | 86 |
| #Binary Variablesⓘ | 0 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 65 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | linear |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 20 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 77 |
| #Linear Constraintsⓘ | 22 |
| #Quadratic Constraintsⓘ | 55 |
| #Polynomial Constraintsⓘ | 0 |
| #Signomial Constraintsⓘ | 0 |
| #General Nonlinear Constraintsⓘ | 0 |
| Operands in Gen. Nonlin. Functionsⓘ | |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 595 |
| #Nonlinear Nonzeros in Jacobianⓘ | 440 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 770 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 0 |
| #Blocks in Hessian of Lagrangianⓘ | 1 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 65 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 65 |
| Average blocksize in Hessian of Lagrangianⓘ | 65.0 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 1.0057e-07 |
| Maximal coefficientⓘ | 4.3600e+02 |
| Infeasibility of initial pointⓘ | 9945 |
| Sparsity Jacobianⓘ | 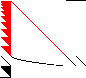 |
| Sparsity Hessian of Lagrangianⓘ |  |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 78 68 10 0 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 87 87 0 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 616 176 440 0
*
* Solve m using NLP minimizing objvar;
Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51,x52,x53
,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68,x69,x70
,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80,x81,x82,x83,x84,x85,x86
,objvar;
Positive Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17
,x18,x19,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34
,x35,x36,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51
,x52,x53,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68
,x69,x70,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80,x81,x82,x83,x84,x85
,x86;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63,e64,e65,e66,e67,e68,e69,e70
,e71,e72,e73,e74,e75,e76,e77,e78;
e1.. 0.2*x2 - x12*(0.2*x2 + 0.32003200320032*x3 + 0.3840672124824*x4 +
0.409692183046145*x5 + 0.409702429449282*x6 + 0.393314332271309*x7 +
0.367084193942431*x8 + 0.335603041715*x9 + 0.302020066201112*x10 +
0.268435410656179*x11) =E= 0;
e2.. 0.32003200320032*x3 - x13*(0.2*x2 + 0.32003200320032*x3 + 0.3840672124824*
x4 + 0.409692183046145*x5 + 0.409702429449282*x6 + 0.393314332271309*x7 +
0.367084193942431*x8 + 0.335603041715*x9 + 0.302020066201112*x10 +
0.268435410656179*x11) =E= 0;
e3.. 0.0399839983998399*x3 - x14*(0.0399839983998399*x3 + 0.0959807923180794*x4
+ 0.153596150395582*x5 + 0.204825598716796*x6 + 0.245821457669569*x7 +
0.275347581122294*x8 + 0.2937261297672*x9 + 0.302133422913057*x10 +
0.302140983052761*x11) =E= 0;
e4.. 0.3840672124824*x4 - x15*(0.2*x2 + 0.32003200320032*x3 + 0.3840672124824*
x4 + 0.409692183046145*x5 + 0.409702429449282*x6 + 0.393314332271309*x7 +
0.367084193942431*x8 + 0.335603041715*x9 + 0.302020066201112*x10 +
0.268435410656179*x11) =E= 0;
e5.. 0.0959807923180794*x4 - x16*(0.0399839983998399*x3 + 0.0959807923180794*x4
+ 0.153596150395582*x5 + 0.204825598716796*x6 + 0.245821457669569*x7 +
0.275347581122294*x8 + 0.2937261297672*x9 + 0.302133422913057*x10 +
0.302140983052761*x11) =E= 0;
e6.. 0.00799040096048009*x4 - x17*(0.00799040096048009*x4 + 0.0255769561603844*
x5 + 0.0511679852758392*x6 + 0.0818892538741687*x7 + 0.114670766025168*x8
+ 0.146807956791712*x9 + 0.176200402504464*x10 + 0.201402121569511*x11)
=E= 0;
e7.. 0.409692183046145*x5 - x18*(0.2*x2 + 0.32003200320032*x3 + 0.3840672124824
*x4 + 0.409692183046145*x5 + 0.409702429449282*x6 + 0.393314332271309*x7
+ 0.367084193942431*x8 + 0.335603041715*x9 + 0.302020066201112*x10 +
0.268435410656179*x11) =E= 0;
e8.. 0.153596150395582*x5 - x19*(0.0399839983998399*x3 + 0.0959807923180794*x4
+ 0.153596150395582*x5 + 0.204825598716796*x6 + 0.245821457669569*x7 +
0.275347581122294*x8 + 0.2937261297672*x9 + 0.302133422913057*x10 +
0.302140983052761*x11) =E= 0;
e9.. 0.0255769561603844*x5 - x20*(0.00799040096048009*x4 + 0.0255769561603844*
x5 + 0.0511679852758392*x6 + 0.0818892538741687*x7 + 0.114670766025168*x8
+ 0.146807956791712*x9 + 0.176200402504464*x10 + 0.201402121569511*x11)
=E= 0;
e10.. 0.001596161920384*x5 - x21*(0.001596161920384*x5 + 0.00638720256256101*x6
+ 0.0153350375081317*x7 + 0.0286354282546281*x8 + 0.0458315860606947*x9
+ 0.0660172990246554*x10 + 0.0880472935145168*x11) =E= 0;
e11.. 0.409702429449282*x6 - x22*(0.2*x2 + 0.32003200320032*x3 +
0.3840672124824*x4 + 0.409692183046145*x5 + 0.409702429449282*x6 +
0.393314332271309*x7 + 0.367084193942431*x8 + 0.335603041715*x9 +
0.302020066201112*x10 + 0.268435410656179*x11) =E= 0;
e12.. 0.204825598716796*x6 - x23*(0.0399839983998399*x3 + 0.0959807923180794*x4
+ 0.153596150395582*x5 + 0.204825598716796*x6 + 0.245821457669569*x7 +
0.275347581122294*x8 + 0.2937261297672*x9 + 0.302133422913057*x10 +
0.302140983052761*x11) =E= 0;
e13.. 0.0511679852758392*x6 - x24*(0.00799040096048009*x4 + 0.0255769561603844*
x5 + 0.0511679852758392*x6 + 0.0818892538741687*x7 + 0.114670766025168*x8
+ 0.146807956791712*x9 + 0.176200402504464*x10 + 0.201402121569511*x11)
=E= 0;
e14.. 0.00638720256256101*x6 - x25*(0.001596161920384*x5 + 0.00638720256256101*
x6 + 0.0153350375081317*x7 + 0.0286354282546281*x8 + 0.0458315860606947*
x9 + 0.0660172990246554*x10 + 0.0880472935145168*x11) =E= 0;
e15.. 0.000318721407871794*x6 - x26*(0.000318721407871794*x6 +
0.00153062807182051*x7 + 0.00428779555860749*x8 + 0.00915141635884911*x9
+ 0.0164795558845939*x10 + 0.0263778458318911*x11) =E= 0;
e16.. 0.393314332271309*x7 - x27*(0.2*x2 + 0.32003200320032*x3 +
0.3840672124824*x4 + 0.409692183046145*x5 + 0.409702429449282*x6 +
0.393314332271309*x7 + 0.367084193942431*x8 + 0.335603041715*x9 +
0.302020066201112*x10 + 0.268435410656179*x11) =E= 0;
e17.. 0.245821457669569*x7 - x28*(0.0399839983998399*x3 + 0.0959807923180794*x4
+ 0.153596150395582*x5 + 0.204825598716796*x6 + 0.245821457669569*x7 +
0.275347581122294*x8 + 0.2937261297672*x9 + 0.302133422913057*x10 +
0.302140983052761*x11) =E= 0;
e18.. 0.0818892538741687*x7 - x29*(0.00799040096048009*x4 + 0.0255769561603844*
x5 + 0.0511679852758392*x6 + 0.0818892538741687*x7 + 0.114670766025168*x8
+ 0.146807956791712*x9 + 0.176200402504464*x10 + 0.201402121569511*x11)
=E= 0;
e19.. 0.0153350375081317*x7 - x30*(0.001596161920384*x5 + 0.00638720256256101*
x6 + 0.0153350375081317*x7 + 0.0286354282546281*x8 + 0.0458315860606947*
x9 + 0.0660172990246554*x10 + 0.0880472935145168*x11) =E= 0;
e20.. 0.00153062807182051*x7 - x31*(0.000318721407871794*x6 +
0.00153062807182051*x7 + 0.00428779555860749*x8 + 0.00915141635884911*x9
+ 0.0164795558845939*x10 + 0.0263778458318911*x11) =E= 0;
e21.. 6.36167292350403e-5*x7 - x32*(6.36167292350403e-5*x7 +
0.00035646756425478*x8 + 0.00114135256538535*x9 + 0.00274075394854443*x10
+ 0.00548438828108048*x11) =E= 0;
e22.. 0.367084193942431*x8 - x33*(0.2*x2 + 0.32003200320032*x3 +
0.3840672124824*x4 + 0.409692183046145*x5 + 0.409702429449282*x6 +
0.393314332271309*x7 + 0.367084193942431*x8 + 0.335603041715*x9 +
0.302020066201112*x10 + 0.268435410656179*x11) =E= 0;
e23.. 0.275347581122294*x8 - x34*(0.0399839983998399*x3 + 0.0959807923180794*x4
+ 0.153596150395582*x5 + 0.204825598716796*x6 + 0.245821457669569*x7 +
0.275347581122294*x8 + 0.2937261297672*x9 + 0.302133422913057*x10 +
0.302140983052761*x11) =E= 0;
e24.. 0.114670766025168*x8 - x35*(0.00799040096048009*x4 + 0.0255769561603844*
x5 + 0.0511679852758392*x6 + 0.0818892538741687*x7 + 0.114670766025168*x8
+ 0.146807956791712*x9 + 0.176200402504464*x10 + 0.201402121569511*x11)
=E= 0;
e25.. 0.0286354282546281*x8 - x36*(0.001596161920384*x5 + 0.00638720256256101*
x6 + 0.0153350375081317*x7 + 0.0286354282546281*x8 + 0.0458315860606947*
x9 + 0.0660172990246554*x10 + 0.0880472935145168*x11) =E= 0;
e26.. 0.00428779555860749*x8 - x37*(0.000318721407871794*x6 +
0.00153062807182051*x7 + 0.00428779555860749*x8 + 0.00915141635884911*x9
+ 0.0164795558845939*x10 + 0.0263778458318911*x11) =E= 0;
e27.. 0.00035646756425478*x8 - x38*(6.36167292350403e-5*x7 +
0.00035646756425478*x8 + 0.00114135256538535*x9 + 0.00274075394854443*x10
+ 0.00548438828108048*x11) =E= 0;
e28.. 1.26927914843577e-5*x8 - x39*(1.26927914843577e-5*x8 +
8.12907690382152e-5*x9 + 0.000292844463262116*x10 + 0.000781426623017516*
x11) =E= 0;
e29.. 0.335603041715*x9 - x40*(0.2*x2 + 0.32003200320032*x3 + 0.3840672124824*
x4 + 0.409692183046145*x5 + 0.409702429449282*x6 + 0.393314332271309*x7
+ 0.367084193942431*x8 + 0.335603041715*x9 + 0.302020066201112*x10 +
0.268435410656179*x11) =E= 0;
e30.. 0.2937261297672*x9 - x41*(0.0399839983998399*x3 + 0.0959807923180794*x4
+ 0.153596150395582*x5 + 0.204825598716796*x6 + 0.245821457669569*x7 +
0.275347581122294*x8 + 0.2937261297672*x9 + 0.302133422913057*x10 +
0.302140983052761*x11) =E= 0;
e31.. 0.146807956791712*x9 - x42*(0.00799040096048009*x4 + 0.0255769561603844*
x5 + 0.0511679852758392*x6 + 0.0818892538741687*x7 + 0.114670766025168*x8
+ 0.146807956791712*x9 + 0.176200402504464*x10 + 0.201402121569511*x11)
=E= 0;
e32.. 0.0458315860606947*x9 - x43*(0.001596161920384*x5 + 0.00638720256256101*
x6 + 0.0153350375081317*x7 + 0.0286354282546281*x8 + 0.0458315860606947*
x9 + 0.0660172990246554*x10 + 0.0880472935145168*x11) =E= 0;
e33.. 0.00915141635884911*x9 - x44*(0.000318721407871794*x6 +
0.00153062807182051*x7 + 0.00428779555860749*x8 + 0.00915141635884911*x9
+ 0.0164795558845939*x10 + 0.0263778458318911*x11) =E= 0;
e34.. 0.00114135256538535*x9 - x45*(6.36167292350403e-5*x7 +
0.00035646756425478*x8 + 0.00114135256538535*x9 + 0.00274075394854443*x10
+ 0.00548438828108048*x11) =E= 0;
e35.. 8.12907690382152e-5*x9 - x46*(1.26927914843577e-5*x8 +
8.12907690382152e-5*x9 + 0.000292844463262116*x10 + 0.000781426623017516*
x11) =E= 0;
e36.. 2.53144535458066e-6*x9 - x47*(2.53144535458066e-6*x9 +
1.82409993524627e-5*x10 + 7.30205954460765e-5*x11) =E= 0;
e37.. 0.302020066201112*x10 - x48*(0.2*x2 + 0.32003200320032*x3 +
0.3840672124824*x4 + 0.409692183046145*x5 + 0.409702429449282*x6 +
0.393314332271309*x7 + 0.367084193942431*x8 + 0.335603041715*x9 +
0.302020066201112*x10 + 0.268435410656179*x11) =E= 0;
e38.. 0.302133422913057*x10 - x49*(0.0399839983998399*x3 + 0.0959807923180794*
x4 + 0.153596150395582*x5 + 0.204825598716796*x6 + 0.245821457669569*x7
+ 0.275347581122294*x8 + 0.2937261297672*x9 + 0.302133422913057*x10 +
0.302140983052761*x11) =E= 0;
e39.. 0.176200402504464*x10 - x50*(0.00799040096048009*x4 + 0.0255769561603844*
x5 + 0.0511679852758392*x6 + 0.0818892538741687*x7 + 0.114670766025168*x8
+ 0.146807956791712*x9 + 0.176200402504464*x10 + 0.201402121569511*x11)
=E= 0;
e40.. 0.0660172990246554*x10 - x51*(0.001596161920384*x5 + 0.00638720256256101*
x6 + 0.0153350375081317*x7 + 0.0286354282546281*x8 + 0.0458315860606947*
x9 + 0.0660172990246554*x10 + 0.0880472935145168*x11) =E= 0;
e41.. 0.0164795558845939*x10 - x52*(0.000318721407871794*x6 +
0.00153062807182051*x7 + 0.00428779555860749*x8 + 0.00915141635884911*x9
+ 0.0164795558845939*x10 + 0.0263778458318911*x11) =E= 0;
e42.. 0.00274075394854443*x10 - x53*(6.36167292350403e-5*x7 +
0.00035646756425478*x8 + 0.00114135256538535*x9 + 0.00274075394854443*x10
+ 0.00548438828108048*x11) =E= 0;
e43.. 0.000292844463262116*x10 - x54*(1.26927914843577e-5*x8 +
8.12907690382152e-5*x9 + 0.000292844463262116*x10 + 0.000781426623017516*
x11) =E= 0;
e44.. 1.82409993524627e-5*x10 - x55*(2.53144535458066e-6*x9 +
1.82409993524627e-5*x10 + 7.30205954460765e-5*x11) =E= 0;
e45.. 5.04667648751466e-7*x10 - x56*(5.04667648751466e-7*x10 +
4.04097807027501e-6*x11) =E= 0;
e46.. 0.268435410656179*x11 - x57*(0.2*x2 + 0.32003200320032*x3 +
0.3840672124824*x4 + 0.409692183046145*x5 + 0.409702429449282*x6 +
0.393314332271309*x7 + 0.367084193942431*x8 + 0.335603041715*x9 +
0.302020066201112*x10 + 0.268435410656179*x11) =E= 0;
e47.. 0.302140983052761*x11 - x58*(0.0399839983998399*x3 + 0.0959807923180794*
x4 + 0.153596150395582*x5 + 0.204825598716796*x6 + 0.245821457669569*x7
+ 0.275347581122294*x8 + 0.2937261297672*x9 + 0.302133422913057*x10 +
0.302140983052761*x11) =E= 0;
e48.. 0.201402121569511*x11 - x59*(0.00799040096048009*x4 + 0.0255769561603844*
x5 + 0.0511679852758392*x6 + 0.0818892538741687*x7 + 0.114670766025168*x8
+ 0.146807956791712*x9 + 0.176200402504464*x10 + 0.201402121569511*x11)
=E= 0;
e49.. 0.0880472935145168*x11 - x60*(0.001596161920384*x5 + 0.00638720256256101*
x6 + 0.0153350375081317*x7 + 0.0286354282546281*x8 + 0.0458315860606947*
x9 + 0.0660172990246554*x10 + 0.0880472935145168*x11) =E= 0;
e50.. 0.0263778458318911*x11 - x61*(0.000318721407871794*x6 +
0.00153062807182051*x7 + 0.00428779555860749*x8 + 0.00915141635884911*x9
+ 0.0164795558845939*x10 + 0.0263778458318911*x11) =E= 0;
e51.. 0.00548438828108048*x11 - x62*(6.36167292350403e-5*x7 +
0.00035646756425478*x8 + 0.00114135256538535*x9 + 0.00274075394854443*x10
+ 0.00548438828108048*x11) =E= 0;
e52.. 0.000781426623017516*x11 - x63*(1.26927914843577e-5*x8 +
8.12907690382152e-5*x9 + 0.000292844463262116*x10 + 0.000781426623017516*
x11) =E= 0;
e53.. 7.30205954460765e-5*x11 - x64*(2.53144535458066e-6*x9 +
1.82409993524627e-5*x10 + 7.30205954460765e-5*x11) =E= 0;
e54.. 4.04097807027501e-6*x11 - x65*(5.04667648751466e-7*x10 +
4.04097807027501e-6*x11) =E= 0;
e55.. 1.0056984172397e-7*x11 - 1.0056984172397e-7*x66*x11 =E= 0;
e56.. 0.200000000000001*x2 - 436*x12 - x67 + x77 =E= 0;
e57.. 0.36001600160016*x3 - 436*x13 - 288*x14 - x68 + x78 =E= 0;
e58.. 0.488038405760964*x4 - 436*x15 - 288*x16 - 185*x17 - x69 + x79 =E= 0;
e59.. 0.590461451522498*x5 - 436*x18 - 288*x19 - 185*x20 - 75*x21 - x70
+ x80 =E= 0;
e60.. 0.672401937412355*x6 - 436*x22 - 288*x23 - 185*x24 - 75*x25 - 19*x26
- x71 + x81 =E= 0;
e61.. 0.737954326124241*x7 - 436*x27 - 288*x28 - 185*x29 - 75*x30 - 19*x31
- 4*x32 - x72 + x82 =E= 0;
e62.. 0.790394925258872*x8 - 436*x33 - 288*x34 - 185*x35 - 75*x36 - 19*x37
- 4*x38 - 2*x39 - x73 + x83 =E= 0;
e63.. 0.832345305473249*x9 - 436*x40 - 288*x41 - 185*x42 - 75*x43 - 19*x44
- 4*x45 - 2*x46 - x74 + x84 =E= 0;
e64.. 0.865903090606706*x10 - 436*x48 - 288*x49 - 185*x50 - 75*x51 - 19*x52
- 4*x53 - 2*x54 - x75 + x85 =E= 0;
e65.. 0.892746631672324*x11 - 436*x57 - 288*x58 - 185*x59 - 75*x60 - 19*x61
- 4*x62 - 2*x63 - x76 + x86 =E= 0;
e66.. x2 + 2*x3 + 3*x4 + 4*x5 + 5*x6 + 6*x7 + 7*x8 + 8*x9 + 9*x10 + 10*x11
=E= 10000;
e67.. x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 =G= 436;
e68.. x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 =G= 288;
e69.. x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 =G= 185;
e70.. x5 + x6 + x7 + x8 + x9 + x10 + x11 =G= 75;
e71.. x6 + x7 + x8 + x9 + x10 + x11 =G= 19;
e72.. x7 + x8 + x9 + x10 + x11 =G= 4;
e73.. x8 + x9 + x10 + x11 =G= 2;
e74.. x9 + x10 + x11 =G= 0;
e75.. x10 + x11 =G= 0;
e76.. x11 =G= 0;
e77.. - x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 =E= 0;
e78.. - x67 - x68 - x69 - x70 - x71 - x72 - x73 - x74 - x75 - x76 - x77 - x78
- x79 - x80 - x81 - x82 - x83 - x84 - x85 - x86 + objvar =E= 0;
* set non-default bounds
x2.up = 10000;
x3.up = 10000;
x4.up = 10000;
x5.up = 10000;
x6.up = 10000;
x7.up = 10000;
x8.up = 10000;
x9.up = 10000;
x10.up = 10000;
x11.up = 10000;
x12.up = 1;
x13.up = 1;
x14.up = 1;
x15.up = 1;
x16.up = 1;
x17.up = 1;
x18.up = 1;
x19.up = 1;
x20.up = 1;
x21.up = 1;
x22.up = 1;
x23.up = 1;
x24.up = 1;
x25.up = 1;
x26.up = 1;
x27.up = 1;
x28.up = 1;
x29.up = 1;
x30.up = 1;
x31.up = 1;
x32.up = 1;
x33.up = 1;
x34.up = 1;
x35.up = 1;
x36.up = 1;
x37.up = 1;
x38.up = 1;
x39.up = 1;
x40.up = 1;
x41.up = 1;
x42.up = 1;
x43.up = 1;
x44.up = 1;
x45.up = 1;
x46.up = 1;
x47.up = 1;
x48.up = 1;
x49.up = 1;
x50.up = 1;
x51.up = 1;
x52.up = 1;
x53.up = 1;
x54.up = 1;
x55.up = 1;
x56.up = 1;
x57.up = 1;
x58.up = 1;
x59.up = 1;
x60.up = 1;
x61.up = 1;
x62.up = 1;
x63.up = 1;
x64.up = 1;
x65.up = 1;
x66.up = 1;
x67.up = 1000;
x68.up = 1000;
x69.up = 1000;
x70.up = 1000;
x71.up = 1000;
x72.up = 1000;
x73.up = 1000;
x74.up = 1000;
x75.up = 1000;
x76.up = 1000;
x77.up = 1000;
x78.up = 1000;
x79.up = 1000;
x80.up = 1000;
x81.up = 1000;
x82.up = 1000;
x83.up = 1000;
x84.up = 1000;
x85.up = 1000;
x86.up = 1000;
* set non-default levels
x2.l = 1;
x3.l = 1;
x4.l = 1;
x5.l = 1;
x6.l = 1;
x7.l = 1;
x8.l = 1;
x9.l = 1;
x10.l = 1;
x11.l = 1;
x12.l = 0.01;
x13.l = 0.01;
x14.l = 0.01;
x15.l = 0.01;
x16.l = 0.01;
x17.l = 0.01;
x18.l = 0.01;
x19.l = 0.01;
x20.l = 0.01;
x21.l = 0.01;
x22.l = 0.01;
x23.l = 0.01;
x24.l = 0.01;
x25.l = 0.01;
x26.l = 0.01;
x27.l = 0.01;
x28.l = 0.01;
x29.l = 0.01;
x30.l = 0.01;
x31.l = 0.01;
x32.l = 0.01;
x33.l = 0.01;
x34.l = 0.01;
x35.l = 0.01;
x36.l = 0.01;
x37.l = 0.01;
x38.l = 0.01;
x39.l = 0.01;
x40.l = 0.01;
x41.l = 0.01;
x42.l = 0.01;
x43.l = 0.01;
x44.l = 0.01;
x45.l = 0.01;
x46.l = 0.01;
x47.l = 0.01;
x48.l = 0.01;
x49.l = 0.01;
x50.l = 0.01;
x51.l = 0.01;
x52.l = 0.01;
x53.l = 0.01;
x54.l = 0.01;
x55.l = 0.01;
x56.l = 0.01;
x57.l = 0.01;
x58.l = 0.01;
x59.l = 0.01;
x60.l = 0.01;
x61.l = 0.01;
x62.l = 0.01;
x63.l = 0.01;
x64.l = 0.01;
x65.l = 0.01;
x66.l = 0.01;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set NLP $set NLP NLP
Solve m using %NLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc