MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance etamac
| Formatsⓘ | ams gms mod nl osil py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | -15.83529486 (ANTIGONE) -16.49103820 (BARON) -18.38730842 (COUENNE) -16.39901950 (LINDO) -15.40567054 (SCIP) |
| Referencesⓘ | Manne, Alan S, ETA-MACRO: A Model of Energy-Economy Interactions. In Hitch, Charles J, Ed, Modeling Energy-Economy Interactions: Five Approaches, Resources for the Future, Washington, DC, 1977. |
| Sourceⓘ | GAMS Model Library model etamac |
| Applicationⓘ | Energy |
| Added to libraryⓘ | 31 Jul 2001 |
| Problem typeⓘ | NLP |
| #Variablesⓘ | 97 |
| #Binary Variablesⓘ | 0 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 35 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | nonlinear |
| Objective curvatureⓘ | convex |
| #Nonzeros in Objectiveⓘ | 9 |
| #Nonlinear Nonzeros in Objectiveⓘ | 9 |
| #Constraintsⓘ | 70 |
| #Linear Constraintsⓘ | 61 |
| #Quadratic Constraintsⓘ | 0 |
| #Polynomial Constraintsⓘ | 0 |
| #Signomial Constraintsⓘ | 0 |
| #General Nonlinear Constraintsⓘ | 9 |
| Operands in Gen. Nonlin. Functionsⓘ | log mul vcpower |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 216 |
| #Nonlinear Nonzeros in Jacobianⓘ | 26 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 85 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 35 |
| #Blocks in Hessian of Lagrangianⓘ | 18 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 1 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 3 |
| Average blocksize in Hessian of Lagrangianⓘ | 1.944444 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 7.0000e-02 |
| Maximal coefficientⓘ | 1.0000e+03 |
| Infeasibility of initial pointⓘ | 2814 |
| Sparsity Jacobianⓘ |  |
| Sparsity Hessian of Lagrangianⓘ | 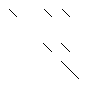 |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 71 70 0 1 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 98 98 0 0 0 0 0 0
* FX 1
*
* Nonzero counts
* Total const NL DLL
* 226 191 35 0
*
* Solve m using NLP minimizing objvar;
Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51,x52,x53
,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68,x69,x70
,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80,x81,x82,x83,x84,x85,x86,x87
,x88,x89,x90,x91,x92,x93,x94,x95,x96,x97,objvar;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63,e64,e65,e66,e67,e68,e69,e70
,e71;
e1.. x10 - 4.91287681*x80 =E= 0;
e2.. x11 - 4.91287681*x81 =E= 0;
e3.. x12 - 4.91287681*x82 =E= 0;
e4.. x13 - 4.91287681*x83 =E= 0;
e5.. x14 - 4.91287681*x84 =E= 0;
e6.. x15 - 4.91287681*x85 =E= 0;
e7.. x16 - 4.91287681*x86 =E= 0;
e8.. x17 - 4.91287681*x87 =E= 0;
e9.. -(0.820744282617518*x10**(-0.342222222222222) + 0.306708090151268*x45**(-
0.427777777777778)*x63**(-0.794444444444445))**(-0.818181818181818) + x27
=E= 0;
e10.. -(0.7206494796327*x11**(-0.342222222222222) + 0.306708090151268*x46**(-
0.427777777777778)*x64**(-0.794444444444445))**(-0.818181818181818) + x28
=E= 0;
e11.. -(0.632761852252708*x12**(-0.342222222222222) + 0.306708090151268*x47**(-
0.427777777777778)*x65**(-0.794444444444445))**(-0.818181818181818) + x29
=E= 0;
e12.. -(0.555592660485018*x13**(-0.342222222222222) + 0.306708090151268*x48**(-
0.427777777777778)*x66**(-0.794444444444445))**(-0.818181818181818) + x30
=E= 0;
e13.. -(0.487834725317074*x14**(-0.342222222222222) + 0.306708090151268*x49**(-
0.427777777777778)*x67**(-0.794444444444445))**(-0.818181818181818) + x31
=E= 0;
e14.. -(0.428340286240339*x15**(-0.342222222222222) + 0.306708090151268*x50**(-
0.427777777777778)*x68**(-0.794444444444445))**(-0.818181818181818) + x32
=E= 0;
e15.. -(0.376101559185243*x16**(-0.342222222222222) + 0.306708090151268*x51**(-
0.427777777777778)*x69**(-0.794444444444445))**(-0.818181818181818) + x33
=E= 0;
e16.. -(0.330233665535262*x17**(-0.342222222222222) + 0.306708090151268*x52**(-
0.427777777777778)*x70**(-0.794444444444445))**(-0.818181818181818) + x34
=E= 0;
e17.. - x35 + x44 =E= -2.038431744;
e18.. 0.8153726976*x35 - x36 + x45 =E= 0;
e19.. 0.8153726976*x36 - x37 + x46 =E= 0;
e20.. 0.8153726976*x37 - x38 + x47 =E= 0;
e21.. 0.8153726976*x38 - x39 + x48 =E= 0;
e22.. 0.8153726976*x39 - x40 + x49 =E= 0;
e23.. 0.8153726976*x40 - x41 + x50 =E= 0;
e24.. 0.8153726976*x41 - x42 + x51 =E= 0;
e25.. 0.8153726976*x42 - x43 + x52 =E= 0;
e26.. - x53 + x62 =E= -40.76863488;
e27.. 0.8153726976*x53 - x54 + x63 =E= 0;
e28.. 0.8153726976*x54 - x55 + x64 =E= 0;
e29.. 0.8153726976*x55 - x56 + x65 =E= 0;
e30.. 0.8153726976*x56 - x57 + x66 =E= 0;
e31.. 0.8153726976*x57 - x58 + x67 =E= 0;
e32.. 0.8153726976*x58 - x59 + x68 =E= 0;
e33.. 0.8153726976*x59 - x60 + x69 =E= 0;
e34.. 0.8153726976*x60 - x61 + x70 =E= 0;
e35.. - 0.8153726976*x1 + x2 - x10 =E= 0;
e36.. - 0.8153726976*x2 + x3 - x11 =E= 0;
e37.. - 0.8153726976*x3 + x4 - x12 =E= 0;
e38.. - 0.8153726976*x4 + x5 - x13 =E= 0;
e39.. - 0.8153726976*x5 + x6 - x14 =E= 0;
e40.. - 0.8153726976*x6 + x7 - x15 =E= 0;
e41.. - 0.8153726976*x7 + x8 - x16 =E= 0;
e42.. - 0.8153726976*x8 + x9 - x17 =E= 0;
e43.. -(0.612508399277048 + 0.306708090151268*x44**(-0.427777777777778)*x62**(-
0.794444444444445))**(-0.818181818181818) + x18 =E= 3.4653339648;
e44.. - 0.8153726976*x18 + x19 - x27 =E= 0;
e45.. - 0.8153726976*x19 + x20 - x28 =E= 0;
e46.. - 0.8153726976*x20 + x21 - x29 =E= 0;
e47.. - 0.8153726976*x21 + x22 - x30 =E= 0;
e48.. - 0.8153726976*x22 + x23 - x31 =E= 0;
e49.. - 0.8153726976*x23 + x24 - x32 =E= 0;
e50.. - 0.8153726976*x24 + x25 - x33 =E= 0;
e51.. - 0.8153726976*x25 + x26 - x34 =E= 0;
e52.. - 52.550502505*x35 - 4.9683636144*x53 + 1000*x89 =E= 0;
e53.. - 55.2311062705602*x36 - 5.48547488997641*x54 + 1000*x90 =E= 0;
e54.. - 58.0484477684999*x37 - 6.05640752245858*x55 + 1000*x91 =E= 0;
e55.. - 61.0095019973984*x38 - 6.68676328190259*x56 + 1000*x92 =E= 0;
e56.. - 64.1215997508617*x39 - 7.38272697509128*x57 + 1000*x93 =E= 0;
e57.. - 67.3924457666453*x40 - 8.15112712846509*x58 + 1000*x94 =E= 0;
e58.. - 70.8301378015635*x41 - 8.99950298698105*x59 + 1000*x95 =E= 0;
e59.. - 74.4431866794111*x42 - 9.93617848626683*x60 + 1000*x96 =E= 0;
e60.. - 78.2405373615315*x43 - 10.970343923856*x61 + 1000*x97 =E= 0;
e61.. x18 - x71 - x80 - x89 =E= 0;
e62.. x19 - x72 - x81 - x90 =E= 0;
e63.. x20 - x73 - x82 - x91 =E= 0;
e64.. x21 - x74 - x83 - x92 =E= 0;
e65.. x22 - x75 - x84 - x93 =E= 0;
e66.. x23 - x76 - x85 - x94 =E= 0;
e67.. x24 - x77 - x86 - x95 =E= 0;
e68.. x25 - x78 - x87 - x96 =E= 0;
e69.. x26 - x79 - x88 - x97 =E= 0;
e70.. 0.07*x9 - x88 =L= 0;
e71.. -(0.8153726976*log(x71) + 0.664832635991501*log(x72) + 0.542086379860909*
log(x73) + 0.442002433879407*log(x74) + 0.360396716858018*log(x75) +
0.293857643230706*log(x76) + 0.239603499271399*log(x77) +
0.19536615155532*log(x78) + 3.98240565033479*log(x79)) - objvar =E= 0;
* set non-default bounds
x1.fx = 12.32657617084;
x2.lo = 10.9;
x3.lo = 10.9;
x4.lo = 10.9;
x5.lo = 10.9;
x6.lo = 10.9;
x7.lo = 10.9;
x8.lo = 10.9;
x9.lo = 10.9;
x10.lo = 1.0317041301;
x11.lo = 1.0317041301;
x12.lo = 1.0317041301;
x13.lo = 1.0317041301;
x14.lo = 1.0317041301;
x15.lo = 1.0317041301;
x16.lo = 1.0317041301;
x17.lo = 1.0317041301;
x18.lo = 4.25;
x19.lo = 4.25;
x20.lo = 4.25;
x21.lo = 4.25;
x22.lo = 4.25;
x23.lo = 4.25;
x24.lo = 4.25;
x25.lo = 4.25;
x26.lo = 4.25;
x27.lo = 0.508311836408595;
x28.lo = 0.589272733608307;
x29.lo = 0.683128602764001;
x30.lo = 0.79193327859709;
x31.lo = 0.918067718453005;
x32.lo = 1.06429210445432;
x33.lo = 1.23380624417608;
x34.lo = 1.43031959158279;
x35.lo = 2.5;
x36.lo = 2.5;
x37.lo = 2.5;
x38.lo = 2.5;
x39.lo = 2.5;
x40.lo = 2.5;
x41.lo = 2.5;
x42.lo = 2.5;
x43.lo = 2.5;
x44.lo = 0.257926032525;
x45.lo = 0.299006962593291;
x46.lo = 0.346631019769593;
x47.lo = 0.401840354567059;
x48.lo = 0.465843105057112;
x49.lo = 0.540039834384121;
x50.lo = 0.626054179090777;
x51.lo = 0.725768378927107;
x52.lo = 0.841364465636933;
x53.lo = 50;
x54.lo = 50;
x55.lo = 50;
x56.lo = 50;
x57.lo = 50;
x58.lo = 50;
x59.lo = 50;
x60.lo = 50;
x61.lo = 50;
x62.lo = 5.1585206505;
x63.lo = 5.98013925186582;
x64.lo = 6.93262039539185;
x65.lo = 8.03680709134119;
x66.lo = 9.31686210114223;
x67.lo = 10.8007966876824;
x68.lo = 12.5210835818155;
x69.lo = 14.5153675785421;
x70.lo = 16.8272893127387;
x71.lo = 3.2;
x72.lo = 3.2;
x73.lo = 3.2;
x74.lo = 3.2;
x75.lo = 3.2;
x76.lo = 3.2;
x77.lo = 3.2;
x78.lo = 3.2;
x79.lo = 3.2;
x80.lo = 0.7;
x81.lo = 0.7;
x82.lo = 0.7;
x83.lo = 0.7;
x84.lo = 0.7;
x85.lo = 0.7;
x86.lo = 0.7;
x87.lo = 0.7;
x88.lo = 0.7;
* set non-default levels
x2.l = 14.6486885348509;
x3.l = 16.9818448409483;
x4.l = 19.6866124578966;
x5.l = 22.8221794332309;
x6.l = 26.4571609359673;
x7.l = 30.6711007526496;
x8.l = 35.5562119327899;
x9.l = 41.2193946739997;
x18.l = 4.926914815775;
x19.l = 5.71164461221252;
x20.l = 6.62136152055325;
x21.l = 7.67597274734501;
x22.l = 8.89855620103042;
x23.l = 10.3158655025561;
x24.l = 11.958915431079;
x25.l = 13.8636606159961;
x26.l = 16.0717823270182;
x35.l = 2.89818518575;
x36.l = 3.35979094836031;
x37.l = 3.89491854150191;
x38.l = 4.51527808667354;
x39.l = 5.23444482413554;
x40.l = 6.06815617797415;
x41.l = 7.03465613592881;
x42.l = 8.15509447999769;
x43.l = 9.45398960412836;
x53.l = 57.963703715;
x54.l = 67.1958189672061;
x55.l = 77.8983708300382;
x56.l = 90.3055617334707;
x57.l = 104.688896482711;
x58.l = 121.363123559483;
x59.l = 140.693122718576;
x60.l = 163.101889599954;
x61.l = 189.079792082567;
x71.l = 3.70967703776;
x72.l = 4.30053241390119;
x73.l = 4.98549573312245;
x74.l = 5.77955595094213;
x75.l = 6.70008937489349;
x76.l = 7.76723990780692;
x77.l = 9.00435985398888;
x78.l = 10.438520934397;
x79.l = 12.1011066932843;
x80.l = 0.81149185201;
x81.l = 0.940741465540885;
x82.l = 1.09057719162054;
x83.l = 1.26427786426859;
x84.l = 1.46564455075795;
x85.l = 1.69908372983276;
x86.l = 1.96970371806007;
x87.l = 2.28342645439935;
x88.l = 2.64711708915594;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set NLP $set NLP NLP
Solve m using %NLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc