MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance kall_circlespolygons_c1p5a
A set of circles and convex polygons are to be cut from rectangular design plates to be produced, or from a set of stocked rectangles of known geometric dimensions. The objective is to minimize the area of the design rectangles. The design plates are subject to lower and upper bounds of their widths and lengths. The objects are free of any orientation restrictions.
| Formatsⓘ | ams gms lp mod nl osil pip py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 0.00000000 (ANTIGONE) 0.00000000 (BARON) 0.00000000 (COUENNE) 2.03191261 (GUROBI) 0.00000000 (LINDO) 0.25087228 (SCIP) |
| Referencesⓘ | Kallrath, Josef, Cutting circles and polygons from area-minimizing rectangles, Journal of Global Optimization, 43:2-3, 2009, 299-328. |
| Sourceⓘ | ANTIGONE test library model Other_MIQCQP/kall_circlespolygons_c1p5a |
| Applicationⓘ | Geometry |
| Added to libraryⓘ | 15 Aug 2014 |
| Problem typeⓘ | QCP |
| #Variablesⓘ | 158 |
| #Binary Variablesⓘ | 0 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 68 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | linear |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 1 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 174 |
| #Linear Constraintsⓘ | 68 |
| #Quadratic Constraintsⓘ | 106 |
| #Polynomial Constraintsⓘ | 0 |
| #Signomial Constraintsⓘ | 0 |
| #General Nonlinear Constraintsⓘ | 0 |
| Operands in Gen. Nonlin. Functionsⓘ | |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 619 |
| #Nonlinear Nonzeros in Jacobianⓘ | 212 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 212 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 10 |
| #Blocks in Hessian of Lagrangianⓘ | 11 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 1 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 14 |
| Average blocksize in Hessian of Lagrangianⓘ | 6.181818 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 1.6667e-01 |
| Maximal coefficientⓘ | 1.2000e+00 |
| Infeasibility of initial pointⓘ | 7.084 |
| Sparsity Jacobianⓘ | 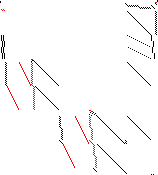 |
| Sparsity Hessian of Lagrangianⓘ | 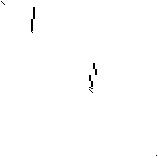 |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 174 145 0 29 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 158 158 0 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 619 407 212 0
*
* Solve m using NLP minimizing objvar;
Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51,x52,x53
,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68,x69,x70
,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80,x81,x82,x83,x84,x85,x86,x87
,x88,x89,x90,x91,x92,x93,x94,x95,x96,x97,x98,x99,x100,x101,x102,x103
,x104,x105,x106,x107,x108,x109,x110,x111,x112,x113,x114,x115,x116
,x117,x118,x119,x120,x121,x122,x123,x124,x125,x126,x127,x128,x129
,x130,x131,x132,x133,x134,x135,x136,x137,x138,x139,x140,x141,x142
,x143,x144,x145,x146,x147,x148,x149,x150,x151,x152,x153,x154,x155
,x156,x157,objvar;
Positive Variables x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19,x60
,x61,x62,x63,x64,x65,x66,x67,x68,x69,x70,x71,x72,x73,x74,x75,x128
,x129,x130,x131,x132,x133,x134,x135,x136,x137,x138,x139,x140,x141
,x142,x143,x144,x145,x146,x147,x148,x149,x150,x151,x152,x153,x154
,x155,x156,x157;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63,e64,e65,e66,e67,e68,e69,e70
,e71,e72,e73,e74,e75,e76,e77,e78,e79,e80,e81,e82,e83,e84,e85,e86,e87
,e88,e89,e90,e91,e92,e93,e94,e95,e96,e97,e98,e99,e100,e101,e102,e103
,e104,e105,e106,e107,e108,e109,e110,e111,e112,e113,e114,e115,e116
,e117,e118,e119,e120,e121,e122,e123,e124,e125,e126,e127,e128,e129
,e130,e131,e132,e133,e134,e135,e136,e137,e138,e139,e140,e141,e142
,e143,e144,e145,e146,e147,e148,e149,e150,e151,e152,e153,e154,e155
,e156,e157,e158,e159,e160,e161,e162,e163,e164,e165,e166,e167,e168
,e169,e170,e171,e172,e173,e174;
e1.. - x1 + objvar =E= -8.5238934211693;
e2.. -x156*x157 + x1 =E= 0;
e3.. x126 - x156 =L= -1.2;
e4.. x127 - x157 =L= -1.2;
e5.. - 0.166666666666667*x128 - 0.166666666666667*x130
- 0.166666666666667*x132 - 0.166666666666667*x134
- 0.166666666666667*x136 - 0.166666666666667*x138 + x152 =E= 0;
e6.. - 0.166666666666667*x129 - 0.166666666666667*x131
- 0.166666666666667*x133 - 0.166666666666667*x135
- 0.166666666666667*x137 - 0.166666666666667*x139 + x153 =E= 0;
e7.. - 0.166666666666667*x140 - 0.166666666666667*x142
- 0.166666666666667*x144 - 0.166666666666667*x146
- 0.166666666666667*x148 - 0.166666666666667*x150 + x154 =E= 0;
e8.. - 0.166666666666667*x141 - 0.166666666666667*x143
- 0.166666666666667*x145 - 0.166666666666667*x147
- 0.166666666666667*x149 - 0.166666666666667*x151 + x155 =E= 0;
e9.. x2*x2 + x4*x4 =E= 1;
e10.. x3*x3 + x5*x5 =E= 1;
e11.. x128 - x156 =L= 0;
e12.. x129 - x157 =L= 0;
e13.. x130 - x156 =L= 0;
e14.. x131 - x157 =L= 0;
e15.. x132 - x156 =L= 0;
e16.. x133 - x157 =L= 0;
e17.. x134 - x156 =L= 0;
e18.. x135 - x157 =L= 0;
e19.. x136 - x156 =L= 0;
e20.. x137 - x157 =L= 0;
e21.. x138 - x156 =L= 0;
e22.. x139 - x157 =L= 0;
e23.. x140 - x156 =L= 0;
e24.. x141 - x157 =L= 0;
e25.. x142 - x156 =L= 0;
e26.. x143 - x157 =L= 0;
e27.. x144 - x156 =L= 0;
e28.. x145 - x157 =L= 0;
e29.. x146 - x156 =L= 0;
e30.. x147 - x157 =L= 0;
e31.. x148 - x156 =L= 0;
e32.. x149 - x157 =L= 0;
e33.. x150 - x156 =L= 0;
e34.. x151 - x157 =L= 0;
e35.. 0.833333333333333*x2 + 0.75*x4 + x128 - x152 =E= 0;
e36.. - 0.166666666666667*x2 + 0.75*x4 + x130 - x152 =E= 0;
e37.. - 0.666666666666667*x2 + 0.25*x4 + x132 - x152 =E= 0;
e38.. - 0.666666666666667*x2 - 0.25*x4 + x134 - x152 =E= 0;
e39.. - 0.166666666666667*x2 - 0.75*x4 + x136 - x152 =E= 0;
e40.. 0.833333333333333*x2 - 0.75*x4 + x138 - x152 =E= 0;
e41.. 0.833333333333333*x3 + 0.75*x5 + x140 - x154 =E= 0;
e42.. - 0.166666666666667*x3 + 0.75*x5 + x142 - x154 =E= 0;
e43.. - 0.666666666666667*x3 + 0.25*x5 + x144 - x154 =E= 0;
e44.. - 0.666666666666667*x3 - 0.25*x5 + x146 - x154 =E= 0;
e45.. - 0.166666666666667*x3 - 0.75*x5 + x148 - x154 =E= 0;
e46.. 0.833333333333333*x3 - 0.75*x5 + x150 - x154 =E= 0;
e47.. - 0.75*x2 + 0.833333333333333*x4 + x129 - x153 =E= 0;
e48.. - 0.75*x2 - 0.166666666666667*x4 + x131 - x153 =E= 0;
e49.. - 0.25*x2 - 0.666666666666667*x4 + x133 - x153 =E= 0;
e50.. 0.25*x2 - 0.666666666666667*x4 + x135 - x153 =E= 0;
e51.. 0.75*x2 - 0.166666666666667*x4 + x137 - x153 =E= 0;
e52.. 0.75*x2 + 0.833333333333333*x4 + x139 - x153 =E= 0;
e53.. - 0.75*x3 + 0.833333333333333*x5 + x141 - x155 =E= 0;
e54.. - 0.75*x3 - 0.166666666666667*x5 + x143 - x155 =E= 0;
e55.. - 0.25*x3 - 0.666666666666667*x5 + x145 - x155 =E= 0;
e56.. 0.25*x3 - 0.666666666666667*x5 + x147 - x155 =E= 0;
e57.. 0.75*x3 - 0.166666666666667*x5 + x149 - x155 =E= 0;
e58.. 0.75*x3 + 0.833333333333333*x5 + x151 - x155 =E= 0;
e59.. x32*x32 + x33*x33 =E= 1;
e60.. - x33 + x34 =E= 0;
e61.. x32 + x35 =E= 0;
e62.. x32*x20 + x6 + x36 - x128 =E= 0;
e63.. x33*x20 + x7 + x37 - x129 =E= 0;
e64.. x32*x21 + x6 + x38 - x130 =E= 0;
e65.. x33*x21 + x7 + x39 - x131 =E= 0;
e66.. x32*x22 + x6 + x40 - x132 =E= 0;
e67.. x33*x22 + x7 + x41 - x133 =E= 0;
e68.. x32*x23 + x6 + x42 - x134 =E= 0;
e69.. x33*x23 + x7 + x43 - x135 =E= 0;
e70.. x32*x24 + x6 + x44 - x136 =E= 0;
e71.. x33*x24 + x7 + x45 - x137 =E= 0;
e72.. x32*x25 + x6 + x46 - x138 =E= 0;
e73.. x33*x25 + x7 + x47 - x139 =E= 0;
e74.. x32*x26 + x6 + x48 - x140 =E= 0;
e75.. x33*x26 + x7 + x49 - x141 =E= 0;
e76.. x32*x27 + x6 + x50 - x142 =E= 0;
e77.. x33*x27 + x7 + x51 - x143 =E= 0;
e78.. x32*x28 + x6 + x52 - x144 =E= 0;
e79.. x33*x28 + x7 + x53 - x145 =E= 0;
e80.. x32*x29 + x6 + x54 - x146 =E= 0;
e81.. x33*x29 + x7 + x55 - x147 =E= 0;
e82.. x32*x30 + x6 + x56 - x148 =E= 0;
e83.. x33*x30 + x7 + x57 - x149 =E= 0;
e84.. x32*x31 + x6 + x58 - x150 =E= 0;
e85.. x33*x31 + x7 + x59 - x151 =E= 0;
e86.. -x8*x34 + x36 =E= 0;
e87.. -x8*x35 + x37 =E= 0;
e88.. -x9*x34 + x38 =E= 0;
e89.. -x9*x35 + x39 =E= 0;
e90.. -x10*x34 + x40 =E= 0;
e91.. -x10*x35 + x41 =E= 0;
e92.. -x11*x34 + x42 =E= 0;
e93.. -x11*x35 + x43 =E= 0;
e94.. -x12*x34 + x44 =E= 0;
e95.. -x12*x35 + x45 =E= 0;
e96.. -x13*x34 + x46 =E= 0;
e97.. -x13*x35 + x47 =E= 0;
e98.. x14*x34 + x48 =E= 0;
e99.. x14*x35 + x49 =E= 0;
e100.. x15*x34 + x50 =E= 0;
e101.. x15*x35 + x51 =E= 0;
e102.. x16*x34 + x52 =E= 0;
e103.. x16*x35 + x53 =E= 0;
e104.. x17*x34 + x54 =E= 0;
e105.. x17*x35 + x55 =E= 0;
e106.. x18*x34 + x56 =E= 0;
e107.. x18*x35 + x57 =E= 0;
e108.. x19*x34 + x58 =E= 0;
e109.. x19*x35 + x59 =E= 0;
e110.. x90*x90 + x91*x91 =E= 1;
e111.. x92*x92 + x93*x93 =E= 1;
e112.. - x91 + x94 =E= 0;
e113.. - x93 + x96 =E= 0;
e114.. x90 + x95 =E= 0;
e115.. x92 + x97 =E= 0;
e116.. x90*x76 + x60 + x98 - x128 =E= 0;
e117.. x91*x76 + x61 + x99 - x129 =E= 0;
e118.. x90*x77 + x60 + x100 - x130 =E= 0;
e119.. x91*x77 + x61 + x101 - x131 =E= 0;
e120.. x90*x78 + x60 + x102 - x132 =E= 0;
e121.. x91*x78 + x61 + x103 - x133 =E= 0;
e122.. x90*x79 + x60 + x104 - x134 =E= 0;
e123.. x91*x79 + x61 + x105 - x135 =E= 0;
e124.. x90*x80 + x60 + x106 - x136 =E= 0;
e125.. x91*x80 + x61 + x107 - x137 =E= 0;
e126.. x90*x81 + x60 + x108 - x138 =E= 0;
e127.. x91*x81 + x61 + x109 - x139 =E= 0;
e128.. x92*x82 + x62 + x110 - x140 =E= 0;
e129.. x93*x82 + x63 + x111 - x141 =E= 0;
e130.. x92*x83 + x62 + x112 - x142 =E= 0;
e131.. x93*x83 + x63 + x113 - x143 =E= 0;
e132.. x92*x84 + x62 + x114 - x144 =E= 0;
e133.. x93*x84 + x63 + x115 - x145 =E= 0;
e134.. x92*x85 + x62 + x116 - x146 =E= 0;
e135.. x93*x85 + x63 + x117 - x147 =E= 0;
e136.. x92*x86 + x62 + x118 - x148 =E= 0;
e137.. x93*x86 + x63 + x119 - x149 =E= 0;
e138.. x92*x87 + x62 + x120 - x150 =E= 0;
e139.. x93*x87 + x63 + x121 - x151 =E= 0;
e140.. x90*x88 + x60 + x122 - x126 =E= 0;
e141.. x91*x88 + x61 + x123 - x127 =E= 0;
e142.. x92*x89 + x62 + x124 - x126 =E= 0;
e143.. x93*x89 + x63 + x125 - x127 =E= 0;
e144.. -x64*x94 + x98 =E= 0;
e145.. -x64*x95 + x99 =E= 0;
e146.. -x65*x94 + x100 =E= 0;
e147.. -x65*x95 + x101 =E= 0;
e148.. -x66*x94 + x102 =E= 0;
e149.. -x66*x95 + x103 =E= 0;
e150.. -x67*x94 + x104 =E= 0;
e151.. -x67*x95 + x105 =E= 0;
e152.. -x68*x94 + x106 =E= 0;
e153.. -x68*x95 + x107 =E= 0;
e154.. -x69*x94 + x108 =E= 0;
e155.. -x69*x95 + x109 =E= 0;
e156.. -x70*x96 + x110 =E= 0;
e157.. -x70*x97 + x111 =E= 0;
e158.. -x71*x96 + x112 =E= 0;
e159.. -x71*x97 + x113 =E= 0;
e160.. -x72*x96 + x114 =E= 0;
e161.. -x72*x97 + x115 =E= 0;
e162.. -x73*x96 + x116 =E= 0;
e163.. -x73*x97 + x117 =E= 0;
e164.. -x74*x96 + x118 =E= 0;
e165.. -x74*x97 + x119 =E= 0;
e166.. -x75*x96 + x120 =E= 0;
e167.. -x75*x97 + x121 =E= 0;
e168.. 1.2*x94 + x122 =E= 0;
e169.. 1.2*x95 + x123 =E= 0;
e170.. 1.2*x96 + x124 =E= 0;
e171.. 1.2*x97 + x125 =E= 0;
e172.. x126 =L= 4;
e173.. x127 =L= 2;
e174.. x152 - x154 =L= 0;
* set non-default bounds
x1.lo = 1.44; x1.up = 32;
x2.lo = -1; x2.up = 1;
x3.lo = -1; x3.up = 1;
x4.lo = -1; x4.up = 1;
x5.lo = -1; x5.up = 1;
x6.up = 8;
x7.up = 4;
x8.up = 8.94427190999916;
x9.up = 8.94427190999916;
x10.up = 8.94427190999916;
x11.up = 8.94427190999916;
x12.up = 8.94427190999916;
x13.up = 8.94427190999916;
x14.up = 8.94427190999916;
x15.up = 8.94427190999916;
x16.up = 8.94427190999916;
x17.up = 8.94427190999916;
x18.up = 8.94427190999916;
x19.up = 8.94427190999916;
x20.lo = -8.94427190999916; x20.up = 8.94427190999916;
x21.lo = -8.94427190999916; x21.up = 8.94427190999916;
x22.lo = -8.94427190999916; x22.up = 8.94427190999916;
x23.lo = -8.94427190999916; x23.up = 8.94427190999916;
x24.lo = -8.94427190999916; x24.up = 8.94427190999916;
x25.lo = -8.94427190999916; x25.up = 8.94427190999916;
x26.lo = -8.94427190999916; x26.up = 8.94427190999916;
x27.lo = -8.94427190999916; x27.up = 8.94427190999916;
x28.lo = -8.94427190999916; x28.up = 8.94427190999916;
x29.lo = -8.94427190999916; x29.up = 8.94427190999916;
x30.lo = -8.94427190999916; x30.up = 8.94427190999916;
x31.lo = -8.94427190999916; x31.up = 8.94427190999916;
x32.lo = -1; x32.up = 1;
x33.lo = -1; x33.up = 1;
x34.lo = -1; x34.up = 1;
x35.lo = -1; x35.up = 1;
x36.lo = -8.94427190999916; x36.up = 8.94427190999916;
x37.lo = -8.94427190999916; x37.up = 8.94427190999916;
x38.lo = -8.94427190999916; x38.up = 8.94427190999916;
x39.lo = -8.94427190999916; x39.up = 8.94427190999916;
x40.lo = -8.94427190999916; x40.up = 8.94427190999916;
x41.lo = -8.94427190999916; x41.up = 8.94427190999916;
x42.lo = -8.94427190999916; x42.up = 8.94427190999916;
x43.lo = -8.94427190999916; x43.up = 8.94427190999916;
x44.lo = -8.94427190999916; x44.up = 8.94427190999916;
x45.lo = -8.94427190999916; x45.up = 8.94427190999916;
x46.lo = -8.94427190999916; x46.up = 8.94427190999916;
x47.lo = -8.94427190999916; x47.up = 8.94427190999916;
x48.lo = -8.94427190999916; x48.up = 8.94427190999916;
x49.lo = -8.94427190999916; x49.up = 8.94427190999916;
x50.lo = -8.94427190999916; x50.up = 8.94427190999916;
x51.lo = -8.94427190999916; x51.up = 8.94427190999916;
x52.lo = -8.94427190999916; x52.up = 8.94427190999916;
x53.lo = -8.94427190999916; x53.up = 8.94427190999916;
x54.lo = -8.94427190999916; x54.up = 8.94427190999916;
x55.lo = -8.94427190999916; x55.up = 8.94427190999916;
x56.lo = -8.94427190999916; x56.up = 8.94427190999916;
x57.lo = -8.94427190999916; x57.up = 8.94427190999916;
x58.lo = -8.94427190999916; x58.up = 8.94427190999916;
x59.lo = -8.94427190999916; x59.up = 8.94427190999916;
x60.up = 8;
x61.up = 4;
x62.up = 8;
x63.up = 4;
x64.up = 8.94427190999916;
x65.up = 8.94427190999916;
x66.up = 8.94427190999916;
x67.up = 8.94427190999916;
x68.up = 8.94427190999916;
x69.up = 8.94427190999916;
x70.up = 8.94427190999916;
x71.up = 8.94427190999916;
x72.up = 8.94427190999916;
x73.up = 8.94427190999916;
x74.up = 8.94427190999916;
x75.up = 8.94427190999916;
x76.lo = -8.94427190999916; x76.up = 8.94427190999916;
x77.lo = -8.94427190999916; x77.up = 8.94427190999916;
x78.lo = -8.94427190999916; x78.up = 8.94427190999916;
x79.lo = -8.94427190999916; x79.up = 8.94427190999916;
x80.lo = -8.94427190999916; x80.up = 8.94427190999916;
x81.lo = -8.94427190999916; x81.up = 8.94427190999916;
x82.lo = -8.94427190999916; x82.up = 8.94427190999916;
x83.lo = -8.94427190999916; x83.up = 8.94427190999916;
x84.lo = -8.94427190999916; x84.up = 8.94427190999916;
x85.lo = -8.94427190999916; x85.up = 8.94427190999916;
x86.lo = -8.94427190999916; x86.up = 8.94427190999916;
x87.lo = -8.94427190999916; x87.up = 8.94427190999916;
x88.lo = -8.94427190999916; x88.up = 8.94427190999916;
x89.lo = -8.94427190999916; x89.up = 8.94427190999916;
x90.lo = -1; x90.up = 1;
x91.lo = -1; x91.up = 1;
x92.lo = -1; x92.up = 1;
x93.lo = -1; x93.up = 1;
x94.lo = -1; x94.up = 1;
x95.lo = -1; x95.up = 1;
x96.lo = -1; x96.up = 1;
x97.lo = -1; x97.up = 1;
x98.lo = -8.94427190999916; x98.up = 8.94427190999916;
x99.lo = -8.94427190999916; x99.up = 8.94427190999916;
x100.lo = -8.94427190999916; x100.up = 8.94427190999916;
x101.lo = -8.94427190999916; x101.up = 8.94427190999916;
x102.lo = -8.94427190999916; x102.up = 8.94427190999916;
x103.lo = -8.94427190999916; x103.up = 8.94427190999916;
x104.lo = -8.94427190999916; x104.up = 8.94427190999916;
x105.lo = -8.94427190999916; x105.up = 8.94427190999916;
x106.lo = -8.94427190999916; x106.up = 8.94427190999916;
x107.lo = -8.94427190999916; x107.up = 8.94427190999916;
x108.lo = -8.94427190999916; x108.up = 8.94427190999916;
x109.lo = -8.94427190999916; x109.up = 8.94427190999916;
x110.lo = -8.94427190999916; x110.up = 8.94427190999916;
x111.lo = -8.94427190999916; x111.up = 8.94427190999916;
x112.lo = -8.94427190999916; x112.up = 8.94427190999916;
x113.lo = -8.94427190999916; x113.up = 8.94427190999916;
x114.lo = -8.94427190999916; x114.up = 8.94427190999916;
x115.lo = -8.94427190999916; x115.up = 8.94427190999916;
x116.lo = -8.94427190999916; x116.up = 8.94427190999916;
x117.lo = -8.94427190999916; x117.up = 8.94427190999916;
x118.lo = -8.94427190999916; x118.up = 8.94427190999916;
x119.lo = -8.94427190999916; x119.up = 8.94427190999916;
x120.lo = -8.94427190999916; x120.up = 8.94427190999916;
x121.lo = -8.94427190999916; x121.up = 8.94427190999916;
x122.lo = -8.94427190999916; x122.up = 8.94427190999916;
x123.lo = -8.94427190999916; x123.up = 8.94427190999916;
x124.lo = -8.94427190999916; x124.up = 8.94427190999916;
x125.lo = -8.94427190999916; x125.up = 8.94427190999916;
x126.lo = 1.2; x126.up = 6.8;
x127.lo = 1.2; x127.up = 2.8;
x128.up = 8;
x129.up = 4;
x130.up = 8;
x131.up = 4;
x132.up = 8;
x133.up = 4;
x134.up = 8;
x135.up = 4;
x136.up = 8;
x137.up = 4;
x138.up = 8;
x139.up = 4;
x140.up = 8;
x141.up = 4;
x142.up = 8;
x143.up = 4;
x144.up = 8;
x145.up = 4;
x146.up = 8;
x147.up = 4;
x148.up = 8;
x149.up = 4;
x150.up = 8;
x151.up = 4;
x152.up = 8;
x153.up = 4;
x154.up = 8;
x155.up = 4;
x156.up = 8;
x157.up = 4;
objvar.lo = 0; objvar.up = 32;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set NLP $set NLP NLP
Solve m using %NLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc