MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance korcns
| Formatsⓘ | ams gms mod nl osil py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 0.00000000 (ANTIGONE) 0.00000000 (BARON) 0.00000000 (COUENNE) 0.00000000 (SCIP) |
| Referencesⓘ | Lewis, J and Robinson, S, Chapter 11. In Chenery, Hollis B, Robinson, Sherman, and Syrquin, Moshe, Eds, Industrialization and Growth: A Comparative Study, Oxford University Press, London, 1986. |
| Sourceⓘ | GAMS Model Library model korcns |
| Applicationⓘ | General Equilibrium |
| Added to libraryⓘ | 31 Jul 2001 |
| Problem typeⓘ | NLP |
| #Variablesⓘ | 96 |
| #Binary Variablesⓘ | 0 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 71 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective typeⓘ | constant |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 0 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 78 |
| #Linear Constraintsⓘ | 34 |
| #Quadratic Constraintsⓘ | 27 |
| #Polynomial Constraintsⓘ | 1 |
| #Signomial Constraintsⓘ | 11 |
| #General Nonlinear Constraintsⓘ | 5 |
| Operands in Gen. Nonlin. Functionsⓘ | vcpower |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 346 |
| #Nonlinear Nonzeros in Jacobianⓘ | 200 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 173 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 29 |
| #Blocks in Hessian of Lagrangianⓘ | 11 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 2 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 23 |
| Average blocksize in Hessian of Lagrangianⓘ | 6.454545 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 1.0000e-05 |
| Maximal coefficientⓘ | 3.8542e+00 |
| Infeasibility of initial pointⓘ | 337.6 |
| Sparsity Jacobianⓘ | 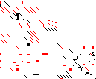 |
| Sparsity Hessian of Lagrangianⓘ |  |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 78 78 0 0 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 96 96 0 0 0 0 0 0
* FX 18
*
* Nonzero counts
* Total const NL DLL
* 346 146 200 0
*
* Solve m using CNS;
Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51,x52,x53
,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68,x69,x70
,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80,x81,x82,x83,x84,x85,x86,x87
,x88,x89,x90,x91,x92,x93,x94,x95,x96;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63,e64,e65,e66,e67,e68,e69,e70
,e71,e72,e73,e74,e75,e76,e77,e78;
e1.. -0.90909*x1*(1.1 + x23) + x5 =E= 0;
e2.. -0.81466*x1*(1.22751 + x23) + x6 =E= 0;
e3.. -0.92521*x1*(1.08084 + x23) + x7 =E= 0;
e4.. - x1 + x8 =E= 0;
e5.. - x1 + x9 =E= 0;
e6.. - x1 + x10 =E= 0;
e7.. x17*x25 - (x2*x31 + x5*x37) =E= 0;
e8.. x18*x26 - (x3*x32 + x6*x38) =E= 0;
e9.. x19*x27 - (x4*x33 + x7*x39) =E= 0;
e10.. x14*x28 - (x2*x31 + x8*x34) =E= 0;
e11.. x15*x29 - (x3*x32 + x9*x35) =E= 0;
e12.. x16*x30 - (x4*x33 + x10*x36) =E= 0;
e13.. 0.99*x14 - 0.12591*x17 - 0.10353*x18 - 0.02358*x19 - x20 =E= 0;
e14.. 0.9608*x15 - 0.19834*x17 - 0.35524*x18 - 0.11608*x19 - x21 =E= 0;
e15.. 0.95*x16 - 0.01407*x17 - 0.18954*x18 - 0.0839*x19 - x22 =E= 0;
e16.. x11 - 0.93076*x18 - 0.06924*x19 =E= 0;
e17.. x12 - 0.93774*x18 - 0.06226*x19 =E= 0;
e18.. x13 - 0.9308*x18 - 0.0692*x19 =E= 0;
e19.. - 0.33263*x17 - 0.43486*x18 - 0.23251*x19 + x24 =E= 0;
e20.. -0.61447*x49**0.38258*x50**0.0674*x40**0.55002 + x28 =E= 0;
e21.. -1.60111*x53**0.53476*x41**0.46524 + x29 =E= 0;
e22.. -0.52019*x56**0.16234*x57**0.42326*x42**0.4144 + x30 =E= 0;
e23.. x43*x49 - 0.38258*x28*x20 =E= 0;
e24.. 0.5278*x44*x50 - 0.0674*x28*x20 =E= 0;
e25.. 1.21879*x44*x53 - 0.53476*x29*x21 =E= 0;
e26.. 1.11541*x44*x56 - 0.16234*x30*x22 =E= 0;
e27.. x45*x57 - 0.42326*x30*x22 =E= 0;
e28.. - x46 + x49 + x52 + x55 =E= 0;
e29.. - x47 + x50 + x53 + x56 =E= 0;
e30.. - x48 + x51 + x54 + x57 =E= 0;
e31.. -3.85424*(0.86628*x34**1.5 + 0.13372*x31**1.5)**0.666666666666667 + x28
=E= 0;
e32.. -3.51886*(0.84602*x35**1.5 + 0.15398*x32**1.5)**0.666666666666667 + x29
=E= 0;
e33.. -3.23592*(0.82436*x36**1.5 + 0.17564*x33**1.5)**0.666666666666667 + x30
=E= 0;
e34.. x34/x31 - sqr(0.154361176524911*x8/x2) =E= 0;
e35.. x35/x32 - sqr(0.182005153542469*x9/x3) =E= 0;
e36.. x36/x33 - sqr(0.213062254354893*x10/x4) =E= 0;
e37.. -1.59539*sqr(0.2482*x37**0.5 + 0.7518*x31**0.5) + x25 =E= 0;
e38.. -1.34652*(0.05111*x38**(-0.515151515151515) + 0.94889*x32**(-
0.515151515151515))**(-1.94117647058824) + x26 =E= 0;
e39.. -1.01839*(1e-5*x39**(-1.5) + 0.99999*x33**(-1.5))**(-0.666666666666667)
+ x27 =E= 0;
e40.. x37/x31 - sqr(0.330140994945464*x2/x5) =E= 0;
e41.. x38/x32 - (0.0538629345867277*x3/x6)**0.66 =E= 0;
e42.. x39/x33 - (1.0000100001e-5*x4/x7)**0.4 =E= 0;
e43.. - 0.12591*x28 - 0.19834*x29 - 0.01407*x30 + x58 =E= 0;
e44.. - 0.10353*x28 - 0.35524*x29 - 0.18954*x30 + x59 =E= 0;
e45.. - 0.02358*x28 - 0.11608*x29 - 0.0839*x30 + x60 =E= 0;
e46.. x17*x61 - ((0.428123 - 0.428123*x84)*x93 + (0.428123 - 0.428123*x85)*x94)
=E= 0;
e47.. x18*x62 - ((0.291478891 - 0.291478891*x84)*x93 + (0.291478891 -
0.291478891*x85)*x94) =E= 0;
e48.. x19*x63 - ((0.191298109 - 0.191298109*x84)*x93 + (0.191298109 -
0.191298109*x85)*x94) =E= 0;
e49.. x70 =E= 0;
e50.. x71 =E= 0;
e51.. x72 =E= 0;
e52.. x73 - x93 - x94 =E= 0;
e53.. -(x43*x46 + x44*x47 + x45*x48 + x91*x1) + x93 =E= 0;
e54.. -(x20*x28 + x21*x29 + x22*x30 - (x43*x46 + x44*x47 + x45*x48) + x92*x1)
+ x81 - x90 + x94 =E= 0;
e55.. - 0.0891*x93 - 0.0891*x94 + x95 =E= 0;
e56.. x64 - 0.02*x78 =E= 0;
e57.. x65 - 0.07*x78 =E= 0;
e58.. x66 - 0.91*x78 =E= 0;
e59.. x74 - x75 - x76 + x77 - x95 =E= 0;
e60.. -(0.090909*x37 + 0.1853432966*x38 + 0.0747939764*x39)*x1 + x75 =E= 0;
e61.. -(0.90909*x37 + 0.81466*x38 + 0.92521*x39)*x1*x23 + x90 =E= 0;
e62.. -(0.01*x14*x28 + 0.0392*x15*x29 + 0.05*x16*x30) + x76 =E= 0;
e63.. x77 =E= 0;
e64.. -(0.9109*x84*x93 + 0.9109*x85*x94) + x79 =E= 0;
e65.. -(x17*x64 + x18*x65 + x19*x66) + x74 - x80 =E= 0;
e66.. x81 =E= 0;
e67.. -x86*x1 - x79 - x80 - x81 + x83 =E= 0;
e68.. x11*x87 + 0.13*(x70*x17 + x71*x18 + x72*x19) - 0.13*x82 =E= 0;
e69.. x12*x88 + 0.29*(x70*x17 + x71*x18 + x72*x19) - 0.29*x82 =E= 0;
e70.. x13*x89 + 0.58*(x70*x17 + x71*x18 + x72*x19) - 0.58*x82 =E= 0;
e71.. x67 =E= 0;
e72.. x68 - 0.93076*x87 - 0.93774*x88 - 0.9308*x89 =E= 0;
e73.. x69 - 0.06924*x87 - 0.06226*x88 - 0.0692*x89 =E= 0;
e74.. - x34 - x35 - x36 + 0.90909*x37 + 0.81466*x38 + 0.92521*x39 - x86 - x91
- x92 =E= 0;
e75.. x25 - x58 - x61 - x64 - x67 - x70 =E= 0;
e76.. x26 - x59 - x62 - x65 - x68 - x71 =E= 0;
e77.. x27 - x60 - x63 - x66 - x69 - x72 =E= 0;
e78.. -x61**0.47*x62**0.31999*x63**0.21001 + x96 =E= 0;
* set non-default bounds
x1.fx = 1;
x2.lo = 0.01;
x3.lo = 0.01;
x4.lo = 0.01;
x5.lo = 0.01;
x6.lo = 0.01;
x7.lo = 0.01;
x11.lo = 0.01;
x12.lo = 0.01;
x13.lo = 0.01;
x14.lo = 0.01;
x15.lo = 0.01;
x16.lo = 0.01;
x17.lo = 0.01;
x18.lo = 0.01;
x19.lo = 0.01;
x24.fx = 1;
x25.lo = 0.01;
x26.lo = 0.01;
x27.lo = 0.01;
x28.lo = 0.01;
x29.lo = 0.01;
x30.lo = 0.01;
x31.lo = 0.01;
x32.lo = 0.01;
x33.lo = 0.01;
x34.lo = 0.01;
x35.lo = 0.01;
x36.lo = 0.01;
x37.lo = 0.01;
x38.lo = 0.01;
x39.lo = 0.01;
x40.fx = 657.5754;
x41.fx = 338.7076;
x42.fx = 1548.5192;
x43.lo = 0.01;
x44.lo = 0.01;
x45.lo = 0.01;
x46.fx = 2515.9;
x47.fx = 1565.987;
x48.fx = 948.1;
x49.lo = 0.01;
x50.lo = 0.01;
x51.fx = 0;
x52.fx = 0;
x53.lo = 0.01;
x54.fx = 0;
x55.fx = 0;
x56.lo = 0.01;
x57.lo = 0.01;
x58.lo = 0.01;
x59.lo = 0.01;
x60.lo = 0.01;
x73.lo = 0.01;
x78.fx = 141.1519;
x84.fx = 0.06;
x85.fx = 0.06;
x86.fx = 39.1744;
x91.fx = 0;
x92.fx = 58.759;
* set non-default levels
x2.l = 1;
x3.l = 1;
x4.l = 1;
x5.l = 1;
x6.l = 1;
x7.l = 1;
x8.l = 1;
x9.l = 1;
x10.l = 1;
x11.l = 1;
x12.l = 1;
x13.l = 1;
x14.l = 1;
x15.l = 1;
x16.l = 1;
x17.l = 1;
x18.l = 1;
x19.l = 1;
x20.l = 0.737;
x21.l = 0.2911;
x22.l = 0.6625;
x25.l = 711.6443;
x26.l = 930.3509;
x27.l = 497.4428;
x28.l = 657.3677;
x29.l = 840.05;
x30.l = 515.4296;
x31.l = 641.7037;
x32.l = 812.2222;
x33.l = 492.0307;
x34.l = 15.6639;
x35.l = 27.8278;
x36.l = 23.3988;
x37.l = 69.9406;
x38.l = 118.1287;
x39.l = 5.412;
x43.l = 0.074;
x44.l = 0.14;
x45.l = 0.152;
x49.l = 2515.9;
x50.l = 442.643;
x53.l = 767.776;
x56.l = 355.568;
x57.l = 948.1;
x58.l = 256.645;
x59.l = 464.1656;
x60.l = 156.2598;
x61.l = 452.1765;
x62.l = 307.8561;
x63.l = 202.0416;
x64.l = 2.823;
x65.l = 9.8806;
x66.l = 128.4482;
x68.l = 148.4488;
x69.l = 10.6931;
x73.l = 1123.5941;
x74.l = 194.0449;
x75.l = 28.6572;
x76.l = 65.2754;
x79.l = 61.4089;
x80.l = 52.893;
x82.l = 159.1419;
x83.l = 159.1419;
x87.l = 20.6884;
x88.l = 46.1511;
x89.l = 92.3023;
x93.l = 548.7478;
x94.l = 574.8463;
x95.l = 100.1122;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set CNS $set CNS CNS
Solve m using %CNS%
Last updated: 2025-08-07 Git hash: e62cedfc