MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance sssd16-07persp
Stochastic Service System Design. Servers are modeled as M/M/1 queues, and a set of customers must be assigned to the servers which can be operated at different service levels. The objective is to minimize assignment and operating costs. Perspective reformulation of sssd16-07.
| Formatsⓘ | ams gms lp mod nl osil pip py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 289034.96780000 (ANTIGONE) 417188.81050000 (BARON) 250227.06710000 (COUENNE) 417188.77440000 (GUROBI) 417188.81050000 (LINDO) 358638.42570000 (SCIP) 2168.85682500 (SHOT) 417188.39340000 (XPRESS) |
| Referencesⓘ | Elhedhli, Samir, Service System Design with Immobile Servers, Stochastic Demand, and Congestion, Manufacturing & Service Operations Management, 8:1, 2006, 92-97. Günlük, Oktay and Linderoth, Jeff T, Perspective reformulations of mixed integer nonlinear programs with indicator variables, Mathematical Programming, 124:1-2, 2010, 183-205. Günlük, Oktay and Linderoth, Jeff T, Perspective Reformulation and Applications. In Lee, Jon and Leyffer, Sven, Eds, Mixed Integer Nonlinear Programming, Springer, 2012, 61-89. |
| Applicationⓘ | Service System Design |
| Added to libraryⓘ | 24 Feb 2014 |
| Problem typeⓘ | MBQCP |
| #Variablesⓘ | 161 |
| #Binary Variablesⓘ | 133 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 49 |
| #Nonlinear Binary Variablesⓘ | 21 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | linear |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 140 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 72 |
| #Linear Constraintsⓘ | 51 |
| #Quadratic Constraintsⓘ | 21 |
| #Polynomial Constraintsⓘ | 0 |
| #Signomial Constraintsⓘ | 0 |
| #General Nonlinear Constraintsⓘ | 0 |
| Operands in Gen. Nonlin. Functionsⓘ | |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 371 |
| #Nonlinear Nonzeros in Jacobianⓘ | 63 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 126 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 0 |
| #Blocks in Hessian of Lagrangianⓘ | 7 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 7 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 7 |
| Average blocksize in Hessian of Lagrangianⓘ | 7.0 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 5.0500e-01 |
| Maximal coefficientⓘ | 8.1781e+04 |
| Infeasibility of initial pointⓘ | 0.3333 |
| Sparsity Jacobianⓘ | 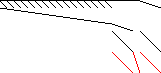 |
| Sparsity Hessian of Lagrangianⓘ |  |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 73 24 0 49 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 162 29 133 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 512 449 63 0
*
* Solve m using MINLP minimizing objvar;
Variables b1,b2,b3,b4,b5,b6,b7,b8,b9,b10,b11,b12,b13,b14,b15,b16,b17,b18,b19
,b20,b21,b22,b23,b24,b25,b26,b27,b28,b29,b30,b31,b32,b33,b34,b35,b36
,b37,b38,b39,b40,b41,b42,b43,b44,b45,b46,b47,b48,b49,b50,b51,b52,b53
,b54,b55,b56,b57,b58,b59,b60,b61,b62,b63,b64,b65,b66,b67,b68,b69,b70
,b71,b72,b73,b74,b75,b76,b77,b78,b79,b80,b81,b82,b83,b84,b85,b86,b87
,b88,b89,b90,b91,b92,b93,b94,b95,b96,b97,b98,b99,b100,b101,b102,b103
,b104,b105,b106,b107,b108,b109,b110,b111,b112,b113,b114,b115,b116
,b117,b118,b119,b120,b121,b122,b123,b124,b125,b126,b127,b128,b129
,b130,b131,b132,b133,x134,x135,x136,x137,x138,x139,x140,x141,x142
,x143,x144,x145,x146,x147,x148,x149,x150,x151,x152,x153,x154,x155
,x156,x157,x158,x159,x160,x161,objvar;
Positive Variables x134,x135,x136,x137,x138,x139,x140,x141,x142,x143,x144
,x145,x146,x147,x148,x149,x150,x151,x152,x153,x154,x155,x156,x157
,x158,x159,x160,x161;
Binary Variables b1,b2,b3,b4,b5,b6,b7,b8,b9,b10,b11,b12,b13,b14,b15,b16,b17
,b18,b19,b20,b21,b22,b23,b24,b25,b26,b27,b28,b29,b30,b31,b32,b33,b34
,b35,b36,b37,b38,b39,b40,b41,b42,b43,b44,b45,b46,b47,b48,b49,b50,b51
,b52,b53,b54,b55,b56,b57,b58,b59,b60,b61,b62,b63,b64,b65,b66,b67,b68
,b69,b70,b71,b72,b73,b74,b75,b76,b77,b78,b79,b80,b81,b82,b83,b84,b85
,b86,b87,b88,b89,b90,b91,b92,b93,b94,b95,b96,b97,b98,b99,b100,b101
,b102,b103,b104,b105,b106,b107,b108,b109,b110,b111,b112,b113,b114
,b115,b116,b117,b118,b119,b120,b121,b122,b123,b124,b125,b126,b127
,b128,b129,b130,b131,b132,b133;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63,e64,e65,e66,e67,e68,e69,e70
,e71,e72,e73;
e1.. - 213.063116318789*b1 - 273.266269308957*b2 - 273.974174702314*b3
- 254.150135436057*b4 - 185.731929048522*b5 - 179.664347941509*b6
- 237.750329788273*b7 - 537.121468653771*b8 - 599.064322370087*b9
- 647.139474601933*b10 - 334.656278986919*b11 - 367.358296540833*b12
- 141.411637746466*b13 - 360.746107012962*b14 - 413.406755015334*b15
- 817.814884544082*b16 - 787.879729353984*b17 - 659.790734814134*b18
- 129.467626164413*b19 - 463.197432726166*b20 - 76.2798654732459*b21
- 92.6304041963229*b22 - 656.979544503091*b23 - 545.816761705456*b24
- 779.467483878278*b25 - 292.944834031572*b26 - 643.908868487291*b27
- 454.262570558583*b28 - 359.628418050031*b29 - 249.165614018324*b30
- 309.573510482173*b31 - 26.8704357917498*b32 - 307.455902574816*b33
- 110.240019364815*b34 - 292.719299621857*b35 - 380.498814693536*b36
- 111.547475796566*b37 - 170.24780915301*b38 - 317.139662731513*b39
- 436.631726254781*b40 - 333.125123720727*b41 - 505.763223945112*b42
- 213.446130466938*b43 - 218.592717682533*b44 - 241.362859574739*b45
- 110.767723212745*b46 - 153.929916757254*b47 - 42.1931799968048*b48
- 150.970037415173*b49 - 708.798337464944*b50 - 603.674904724189*b51
- 704.764096387507*b52 - 147.392997602376*b53 - 549.30947955643*b54
- 71.2061442568205*b55 - 506.349076214288*b56 - 55.8566864444488*b57
- 372.553396170802*b58 - 316.282148724127*b59 - 422.527547001739*b60
- 136.475370007946*b61 - 342.037721074908*b62 - 226.669260720425*b63
- 425.796044889891*b64 - 352.066307741805*b65 - 178.075578035487*b66
- 770.923567714452*b67 - 658.958002502518*b68 - 745.698256364226*b69
- 808.051498329816*b70 - 43.2977732665271*b71 - 355.089484484089*b72
- 294.923700002902*b73 - 421.41698205632*b74 - 156.07903905941*b75
- 347.015757251517*b76 - 245.511452101303*b77 - 86.3864296201078*b78
- 335.699293512738*b79 - 297.182031615534*b80 - 345.872125504266*b81
- 80.1774101234563*b82 - 270.842757092031*b83 - 149.362369607845*b84
- 348.763184821689*b85 - 137.967314173634*b86 - 49.4525994536456*b87
- 450.867970954852*b88 - 471.47080669281*b89 - 461.24773668693*b90
- 556.405313819934*b91 - 34.374298528587*b92 - 613.459413261482*b93
- 492.553739135761*b94 - 781.49028155613*b95 - 330.510227759565*b96
- 646.855838755768*b97 - 515.360830627384*b98 - 463.500876655565*b99
- 367.830152731938*b100 - 421.957579253695*b101 - 300.884945465719*b102
- 424.273071696965*b103 - 241.069021571292*b104 - 479.327877226618*b105
- 249.164006992026*b106 - 420.579677379549*b107 - 339.215571195438*b108
- 611.532890240341*b109 - 394.081036970694*b110 - 515.338037680354*b111
- 547.401615707871*b112 - 272.18661225*b113 - 99.714661105525*b114
- 64.0133197333671*b115 - 378.143072*b116 - 122.880274343504*b117
- 74.2950034949714*b118 - 423.23534075*b119 - 129.143042829026*b120
- 75.6623059288464*b121 - 452.32349625*b122 - 144.695478742473*b123
- 86.8004922924363*b124 - 435.074808*b125 - 143.488032005532*b126
- 87.3989206979294*b127 - 289.71387775*b128 - 101.536870281553*b129
- 63.7552459028209*b130 - 407.39804875*b131 - 136.635688397713*b132
- 83.9269383442227*b133 - 81781.4884544082*x134 - 81781.4884544082*x135
- 81781.4884544082*x136 - 81781.4884544082*x137 - 81781.4884544082*x138
- 81781.4884544082*x139 - 81781.4884544082*x140 + objvar =E= 0;
e2.. 0.758108132*b1 + 1.33888976*b8 + 1.20095942*b15 + 1.132281133*b22
+ 0.540135431*b29 + 0.914702055*b36 + 0.504999442*b43 + 1.289521543*b50
+ 0.637213608*b57 + 1.164412792*b64 + 0.624195834*b71 + 0.531968424*b78
+ 0.766940956*b85 + 1.287734319*b92 + 1.226844689*b99 + 1.318512368*b106
- 1.67275151142857*x141 - 3.34550302285714*x142 - 5.01825453428571*x143
=E= 0;
e3.. 0.758108132*b2 + 1.33888976*b9 + 1.20095942*b16 + 1.132281133*b23
+ 0.540135431*b30 + 0.914702055*b37 + 0.504999442*b44 + 1.289521543*b51
+ 0.637213608*b58 + 1.164412792*b65 + 0.624195834*b72 + 0.531968424*b79
+ 0.766940956*b86 + 1.287734319*b93 + 1.226844689*b100 + 1.318512368*b107
- 1.621886868*x144 - 3.243773736*x145 - 4.865660604*x146 =E= 0;
e4.. 0.758108132*b3 + 1.33888976*b10 + 1.20095942*b17 + 1.132281133*b24
+ 0.540135431*b31 + 0.914702055*b38 + 0.504999442*b45 + 1.289521543*b52
+ 0.637213608*b59 + 1.164412792*b66 + 0.624195834*b73 + 0.531968424*b80
+ 0.766940956*b87 + 1.287734319*b94 + 1.226844689*b101 + 1.318512368*b108
- 1.50291601314286*x147 - 3.00583202628571*x148 - 4.50874803942857*x149
=E= 0;
e5.. 0.758108132*b4 + 1.33888976*b11 + 1.20095942*b18 + 1.132281133*b25
+ 0.540135431*b32 + 0.914702055*b39 + 0.504999442*b46 + 1.289521543*b53
+ 0.637213608*b60 + 1.164412792*b67 + 0.624195834*b74 + 0.531968424*b81
+ 0.766940956*b88 + 1.287734319*b95 + 1.226844689*b102 + 1.318512368*b109
- 1.85077114171429*x150 - 3.70154228342857*x151 - 5.55231342514286*x152
=E= 0;
e6.. 0.758108132*b5 + 1.33888976*b12 + 1.20095942*b19 + 1.132281133*b26
+ 0.540135431*b33 + 0.914702055*b40 + 0.504999442*b47 + 1.289521543*b54
+ 0.637213608*b61 + 1.164412792*b68 + 0.624195834*b75 + 0.531968424*b82
+ 0.766940956*b89 + 1.287734319*b96 + 1.226844689*b103 + 1.318512368*b110
- 1.950768312*x153 - 3.901536624*x154 - 5.852304936*x155 =E= 0;
e7.. 0.758108132*b6 + 1.33888976*b13 + 1.20095942*b20 + 1.132281133*b27
+ 0.540135431*b34 + 0.914702055*b41 + 0.504999442*b48 + 1.289521543*b55
+ 0.637213608*b62 + 1.164412792*b69 + 0.624195834*b76 + 0.531968424*b83
+ 0.766940956*b90 + 1.287734319*b97 + 1.226844689*b104 + 1.318512368*b111
- 1.55890640628571*x156 - 3.11781281257143*x157 - 4.67671921885714*x158
=E= 0;
e8.. 0.758108132*b7 + 1.33888976*b14 + 1.20095942*b21 + 1.132281133*b28
+ 0.540135431*b35 + 0.914702055*b42 + 0.504999442*b49 + 1.289521543*b56
+ 0.637213608*b63 + 1.164412792*b70 + 0.624195834*b77 + 0.531968424*b84
+ 0.766940956*b91 + 1.287734319*b98 + 1.226844689*b105 + 1.318512368*b112
- 1.92106166914286*x159 - 3.84212333828571*x160 - 5.76318500742857*x161
=E= 0;
e9.. b1 + b2 + b3 + b4 + b5 + b6 + b7 =E= 1;
e10.. b8 + b9 + b10 + b11 + b12 + b13 + b14 =E= 1;
e11.. b15 + b16 + b17 + b18 + b19 + b20 + b21 =E= 1;
e12.. b22 + b23 + b24 + b25 + b26 + b27 + b28 =E= 1;
e13.. b29 + b30 + b31 + b32 + b33 + b34 + b35 =E= 1;
e14.. b36 + b37 + b38 + b39 + b40 + b41 + b42 =E= 1;
e15.. b43 + b44 + b45 + b46 + b47 + b48 + b49 =E= 1;
e16.. b50 + b51 + b52 + b53 + b54 + b55 + b56 =E= 1;
e17.. b57 + b58 + b59 + b60 + b61 + b62 + b63 =E= 1;
e18.. b64 + b65 + b66 + b67 + b68 + b69 + b70 =E= 1;
e19.. b71 + b72 + b73 + b74 + b75 + b76 + b77 =E= 1;
e20.. b78 + b79 + b80 + b81 + b82 + b83 + b84 =E= 1;
e21.. b85 + b86 + b87 + b88 + b89 + b90 + b91 =E= 1;
e22.. b92 + b93 + b94 + b95 + b96 + b97 + b98 =E= 1;
e23.. b99 + b100 + b101 + b102 + b103 + b104 + b105 =E= 1;
e24.. b106 + b107 + b108 + b109 + b110 + b111 + b112 =E= 1;
e25.. b113 + b114 + b115 =L= 1;
e26.. b116 + b117 + b118 =L= 1;
e27.. b119 + b120 + b121 =L= 1;
e28.. b122 + b123 + b124 =L= 1;
e29.. b125 + b126 + b127 =L= 1;
e30.. b128 + b129 + b130 =L= 1;
e31.. b131 + b132 + b133 =L= 1;
e32.. - b113 + x141 =L= 0;
e33.. - b114 + x142 =L= 0;
e34.. - b115 + x143 =L= 0;
e35.. - b116 + x144 =L= 0;
e36.. - b117 + x145 =L= 0;
e37.. - b118 + x146 =L= 0;
e38.. - b119 + x147 =L= 0;
e39.. - b120 + x148 =L= 0;
e40.. - b121 + x149 =L= 0;
e41.. - b122 + x150 =L= 0;
e42.. - b123 + x151 =L= 0;
e43.. - b124 + x152 =L= 0;
e44.. - b125 + x153 =L= 0;
e45.. - b126 + x154 =L= 0;
e46.. - b127 + x155 =L= 0;
e47.. - b128 + x156 =L= 0;
e48.. - b129 + x157 =L= 0;
e49.. - b130 + x158 =L= 0;
e50.. - b131 + x159 =L= 0;
e51.. - b132 + x160 =L= 0;
e52.. - b133 + x161 =L= 0;
e53.. x141*b113 + x141*x134 - x134*b113 =L= 0;
e54.. x142*b114 + x142*x134 - x134*b114 =L= 0;
e55.. x143*b115 + x143*x134 - x134*b115 =L= 0;
e56.. x144*b116 + x144*x135 - x135*b116 =L= 0;
e57.. x145*b117 + x145*x135 - x135*b117 =L= 0;
e58.. x146*b118 + x146*x135 - x135*b118 =L= 0;
e59.. x147*b119 + x147*x136 - x136*b119 =L= 0;
e60.. x148*b120 + x148*x136 - x136*b120 =L= 0;
e61.. x149*b121 + x149*x136 - x136*b121 =L= 0;
e62.. x150*b122 + x150*x137 - x137*b122 =L= 0;
e63.. x151*b123 + x151*x137 - x137*b123 =L= 0;
e64.. x152*b124 + x152*x137 - x137*b124 =L= 0;
e65.. x153*b125 + x153*x138 - x138*b125 =L= 0;
e66.. x154*b126 + x154*x138 - x138*b126 =L= 0;
e67.. x155*b127 + x155*x138 - x138*b127 =L= 0;
e68.. x156*b128 + x156*x139 - x139*b128 =L= 0;
e69.. x157*b129 + x157*x139 - x139*b129 =L= 0;
e70.. x158*b130 + x158*x139 - x139*b130 =L= 0;
e71.. x159*b131 + x159*x140 - x140*b131 =L= 0;
e72.. x160*b132 + x160*x140 - x140*b132 =L= 0;
e73.. x161*b133 + x161*x140 - x140*b133 =L= 0;
* set non-default levels
b1.l = 0.142857142857143;
b2.l = 0.142857142857143;
b3.l = 0.142857142857143;
b4.l = 0.142857142857143;
b5.l = 0.142857142857143;
b6.l = 0.142857142857143;
b7.l = 0.142857142857143;
b8.l = 0.142857142857143;
b9.l = 0.142857142857143;
b10.l = 0.142857142857143;
b11.l = 0.142857142857143;
b12.l = 0.142857142857143;
b13.l = 0.142857142857143;
b14.l = 0.142857142857143;
b15.l = 0.142857142857143;
b16.l = 0.142857142857143;
b17.l = 0.142857142857143;
b18.l = 0.142857142857143;
b19.l = 0.142857142857143;
b20.l = 0.142857142857143;
b21.l = 0.142857142857143;
b22.l = 0.142857142857143;
b23.l = 0.142857142857143;
b24.l = 0.142857142857143;
b25.l = 0.142857142857143;
b26.l = 0.142857142857143;
b27.l = 0.142857142857143;
b28.l = 0.142857142857143;
b29.l = 0.142857142857143;
b30.l = 0.142857142857143;
b31.l = 0.142857142857143;
b32.l = 0.142857142857143;
b33.l = 0.142857142857143;
b34.l = 0.142857142857143;
b35.l = 0.142857142857143;
b36.l = 0.142857142857143;
b37.l = 0.142857142857143;
b38.l = 0.142857142857143;
b39.l = 0.142857142857143;
b40.l = 0.142857142857143;
b41.l = 0.142857142857143;
b42.l = 0.142857142857143;
b43.l = 0.142857142857143;
b44.l = 0.142857142857143;
b45.l = 0.142857142857143;
b46.l = 0.142857142857143;
b47.l = 0.142857142857143;
b48.l = 0.142857142857143;
b49.l = 0.142857142857143;
b50.l = 0.142857142857143;
b51.l = 0.142857142857143;
b52.l = 0.142857142857143;
b53.l = 0.142857142857143;
b54.l = 0.142857142857143;
b55.l = 0.142857142857143;
b56.l = 0.142857142857143;
b57.l = 0.142857142857143;
b58.l = 0.142857142857143;
b59.l = 0.142857142857143;
b60.l = 0.142857142857143;
b61.l = 0.142857142857143;
b62.l = 0.142857142857143;
b63.l = 0.142857142857143;
b64.l = 0.142857142857143;
b65.l = 0.142857142857143;
b66.l = 0.142857142857143;
b67.l = 0.142857142857143;
b68.l = 0.142857142857143;
b69.l = 0.142857142857143;
b70.l = 0.142857142857143;
b71.l = 0.142857142857143;
b72.l = 0.142857142857143;
b73.l = 0.142857142857143;
b74.l = 0.142857142857143;
b75.l = 0.142857142857143;
b76.l = 0.142857142857143;
b77.l = 0.142857142857143;
b78.l = 0.142857142857143;
b79.l = 0.142857142857143;
b80.l = 0.142857142857143;
b81.l = 0.142857142857143;
b82.l = 0.142857142857143;
b83.l = 0.142857142857143;
b84.l = 0.142857142857143;
b85.l = 0.142857142857143;
b86.l = 0.142857142857143;
b87.l = 0.142857142857143;
b88.l = 0.142857142857143;
b89.l = 0.142857142857143;
b90.l = 0.142857142857143;
b91.l = 0.142857142857143;
b92.l = 0.142857142857143;
b93.l = 0.142857142857143;
b94.l = 0.142857142857143;
b95.l = 0.142857142857143;
b96.l = 0.142857142857143;
b97.l = 0.142857142857143;
b98.l = 0.142857142857143;
b99.l = 0.142857142857143;
b100.l = 0.142857142857143;
b101.l = 0.142857142857143;
b102.l = 0.142857142857143;
b103.l = 0.142857142857143;
b104.l = 0.142857142857143;
b105.l = 0.142857142857143;
b106.l = 0.142857142857143;
b107.l = 0.142857142857143;
b108.l = 0.142857142857143;
b109.l = 0.142857142857143;
b110.l = 0.142857142857143;
b111.l = 0.142857142857143;
b112.l = 0.142857142857143;
b113.l = 0.333333333333333;
b114.l = 0.333333333333333;
b115.l = 0.333333333333333;
b116.l = 0.333333333333333;
b117.l = 0.333333333333333;
b118.l = 0.333333333333333;
b119.l = 0.333333333333333;
b120.l = 0.333333333333333;
b121.l = 0.333333333333333;
b122.l = 0.333333333333333;
b123.l = 0.333333333333333;
b124.l = 0.333333333333333;
b125.l = 0.333333333333333;
b126.l = 0.333333333333333;
b127.l = 0.333333333333333;
b128.l = 0.333333333333333;
b129.l = 0.333333333333333;
b130.l = 0.333333333333333;
b131.l = 0.333333333333333;
b132.l = 0.333333333333333;
b133.l = 0.333333333333333;
x134.l = 1.86251452376903;
x135.l = 2.04008937802859;
x136.l = 2.62560028150429;
x137.l = 1.42761013897069;
x138.l = 1.2620720008888;
x139.l = 2.31316166033414;
x140.l = 1.30709790321263;
x141.l = 0.216885598111212;
x142.l = 0.216885598111212;
x143.l = 0.216885598111212;
x144.l = 0.223687434188917;
x145.l = 0.223687434188917;
x146.l = 0.223687434188917;
x147.l = 0.241394534940745;
x148.l = 0.241394534940745;
x149.l = 0.241394534940745;
x150.l = 0.196024080919901;
x151.l = 0.196024080919901;
x152.l = 0.196024080919901;
x153.l = 0.185975807488726;
x154.l = 0.185975807488726;
x155.l = 0.185975807488726;
x156.l = 0.232724498779901;
x157.l = 0.232724498779901;
x158.l = 0.232724498779901;
x159.l = 0.188851673985818;
x160.l = 0.188851673985818;
x161.l = 0.188851673985818;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set MINLP $set MINLP MINLP
Solve m using %MINLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc